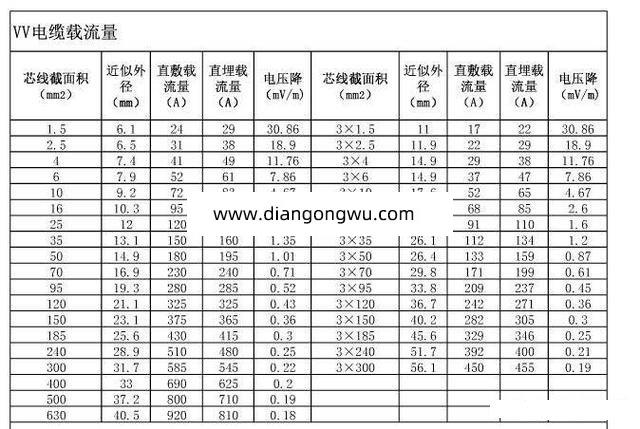
星形接法与三角形接法图及同一种电压不同接法效果对比
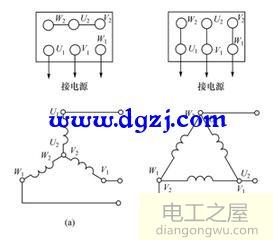
星形接法与三角形接法图
一、同一种输入电压(线电压),采取两种不同的接法时(星形接法、三角形接法);这也就是常见的Y-△启动接法,也就是在启动时为“Y”接法,做正常运行时为△接法,。它们的输入线电压是一样的。设输入的线电压Ue为U,每相的阻抗为IZI,每相的功率因数cosφ;
星形接法时:每相的相电压Up=U/√3,每相的相电流Ip=Up/IZI=U/√3IZI,星形接法时,线电流与相电流相等,即Ie=Ip=U/√3IZI,平均功率P=√3UeIecosφ=U2cosφ/IZI(线电压的平方×cosφ/阻抗),输出转矩Ty∞(Up)2=(U/√3)=U2/3(线电压的平方/3),∞指正比关系。
三角形接法时:每相的相电压Up=U,每相的相电流Ip=Up/IZI=U/√IZI,三角形接法时线电流为相电流的√3倍,即Ie=Ip=√3U/√IZI,输出功率P=√3UeIecosφ=3U2cosφ/IZI(线电压的平方×3×cosφ/阻抗),转矩T△∞(Up)2=U2(线电压的平方)
对比表如下,设线电压为1,阻抗为1,功率因数为1(这并不影响我们的研究,在对比过程中这些量会消掉,我们只关心对比结果)

同一种电压,不同接法效果对比
从以上计算、对比过程我们得出,在同一种输入电压下,三角形接法与星形接法相比,相电压为√3倍关系;线电流为3倍关系,相电流为√3倍广西,平均功率为3倍关系,转矩为3倍关系。这就是采用星-三角形接法用来降低启动电流的原因,不过同时它的启动转矩也降低了,这一点在使用上应该注意。
二、两种输入电压(线电压),采取两种不同接法(星形接法、三角形接法),也就是大电压时采用Y接法,小电压时采用△接法;两种输入的线电压为√3倍关系,即UY=√3U△,而加在每相绕组上的电压是一样的(相电压)。设输入的线电压Uey(星形接法)为U,每相阻抗为IZI,每相的功率因数cosφ
星形接法时,每相的相电压Up=U/√3,每相的相电流Ip=Up/IZI=U/√3IZI,线电流与相电流相等,即Ie=Ip=U/√3IZI,输出功率P=√3UeIecosφ=U2cosφ/IZI(线电压的平方*cosφ/阻抗),输出转矩Ty∞(Up)2=(U/√3)2=U2/3(电压平方/3)
三角形接法时,每相的相电压等于线电压Up=U/√3,每相的相电流Ip=Up/IZI=U/√3IZI,线电流为相电流的√3倍,即Ie=√3Ip=U/√IZI,输出功率P=√3UeIecosφ=U2cosφ/IZI,转矩T△∞(Up)2=(U/√3)2=U2/3(线电压平方/3)。
同上,我们将线电压设为1,阻抗为1,功率因数为1,对比如下

两种电压、两种接法对比
通过上面的计算、对比我们发现,采用两种不同的输入电压时和接法时,三角形接法和星形接法,线电压为1/√3关系,相电压相等,线电流为√3关系,相电流相等,平均功率相等,转矩相等。这就是一种电动机采取两种接法的原因。