数制与各进制数之间的转换

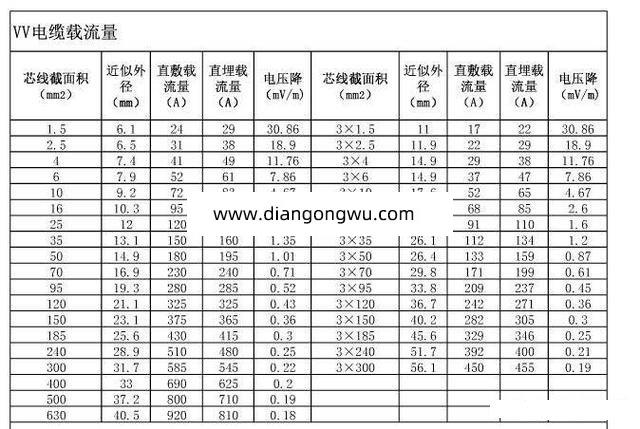
数制与各进制数之间的转换

数制也称计数制，是用一组固定的符号和统一的规则来表示数值的方法。人们通常采用的数制有十进制、二进制、八进制和十六进制。 学习数制，必须首先掌握数码、基数和位权这3个概念。

数码：数制中表示基本数值大小的不同数字符号。例如，十进制有10个数码：0、1、2、3、4、5、6、7、8、9。

基数：数制所使用数码的个数。例如，二进制的基数为2；十进制的基数为10。

位权：数制中某一位上的1所表示数值的大小（所处位置的价值）。例如，十进制的523，5的位权是100，2的位权是10，3的位权是1。

数制的种类:

二进制、八进制、十进制和十六进制。

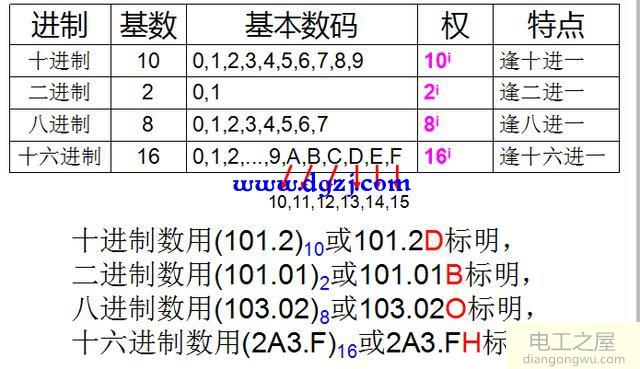
图1

1、把其他进制的数转换成十进制数

方法是：将其它进制按权展开，然后各项相加，就 得到相应的十进制数。

如: （219.1)10=2*102+1*101+9*100+1*10-1

（11010.1)2=1*24+1*23+0*22+1*21+0*20+1*2-1=26.5

（273)8=2*82+7*81+3*80=187

(7AF.A)16=7*162+10*161+15*160+10*16-1=1867.625

图2

十进制小数转换为二进制

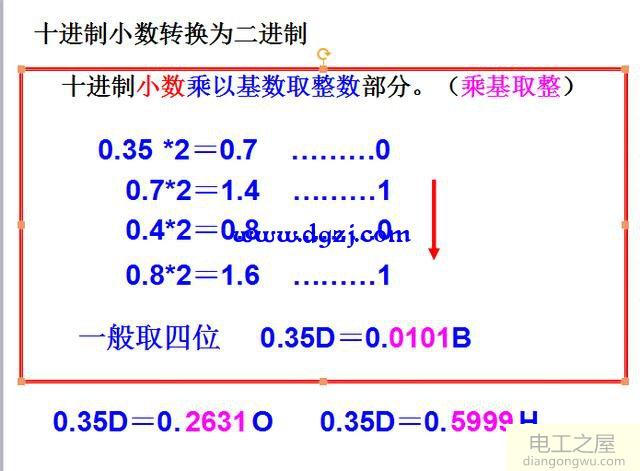
图3

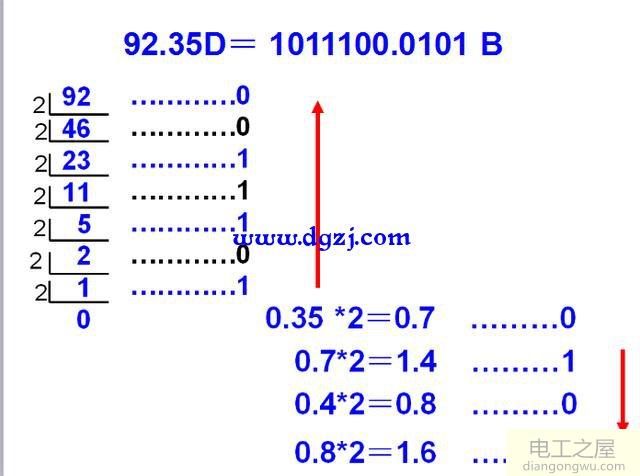
图4

3、二进制转换为八进制十六进制

把二进制数转换为八进制时，从小数点所在位置分别向左向右对每三位二进制位进行分组，不足时补若干个0，然后从左到右把每组的八进制码依次写出，即得转换结果。

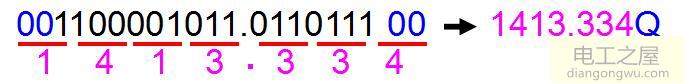
图5

把二进制数转换为十六进制时，从小数点所在位置分别向左向右对每四位二进制位进行分组，不足时补若干个0，然后从左到右把每组的十六进制码依次写出，即得转换结果。

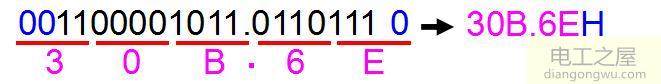
图5

4、八进制十六进制转换为二进制

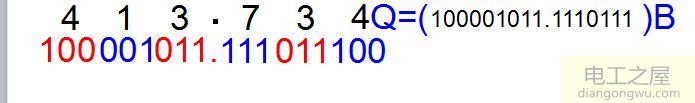
图6