图6. 在3.5 GHz 处+85°C时的温度漂移分布曲线移动并不再与25°C时的分布曲线平行。
通过+85°C对数一致性曲线的线性区的趋势线表示该温度的误差模型。
由于斜率和截距随温度变化导致温度漂移。鉴于这种认识,通过分析器件的总体分布曲线可以总结出一个误差模型。可以建立分布曲线随温度移动的误差表达式,如图6所示。图中画出的通过+85°C对数一致性曲线的线性区的趋势线——误差线,它表示在+85°C时的误差模型。应用该误差线的斜率和截距特性,利用补偿函数关系可抵消这种温度变化。尽管如此,该误差模型仅描述+85°C时温度漂移带来的误差。
大多数的温度漂移发生在+25°C和+85°C之间。对所有温度都普遍适用的误差函数可利用一个温度比例因子k(T)来建立各种温度范围的函数关系,其中k(T)是温度的函数。将补偿误差函数和温度比例因子函数结合起来,组合结果如图7所示。当温度升高的时候,比例因数将跟着变化,从而可消除由于温度漂移上升引起的误差。
图7示出AD8312采用上述误差补偿方法的对数一致性分布。误差补偿前,对数一致性误差为5 dB。误差补偿后,在从-30 dBm 至 0 dBm功率输入范围之间,在整个工作温度范围内对数一致性误差提高到大约±0.5 dB。这种RF功率管理系统可达到的精度是由器件的总体分布曲线确定的。同样的结果对于温度漂移不显著的低温和低频情况也可适用。
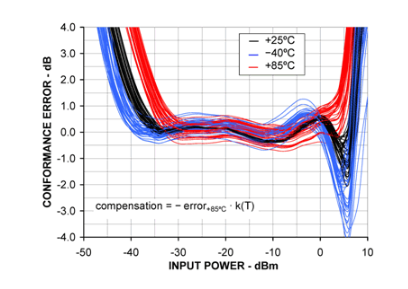
图7. 用补偿误差函数抵消温温度变化引起的误差。
用误差补偿改善整个温度范围内的对数一致性误差。











