零应填充在正确的位置,以把反转反转的振铃保持在脉冲响应最后。
选项1:从脉冲响应右端开始,检查是否有反转。如果没有反转,那么可以在脉冲响应最后点之后从右面填充。如果有反转,那么可以向回搜索,找到反转的信号的稳定位置,可以在稳定的位置填充零,如图9所示。
选项2:一直选择一定比例的脉冲响应,填充零。例如,从末尾在时间间隔5%的位置填充零。这种选项要求已经以足够的频率间隔测量所有原始S参数数据,以便以稳定的记录百分比为所有参数提供时间间隔,在这里将插入零填充。这也意味着在零填充点之外已经包括足够的时间,以便在这个点以后,所有反转的数据将从左到右稳定。图8和图9显示了执行零填充前和执行零填充后的结果。
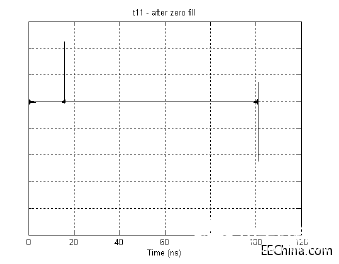
图9. 这是再采样的s11的脉冲响应。右端保留了早期振铃。
再采样的S参数与原始S参数匹配得非常好,如图10中的频域图所示。
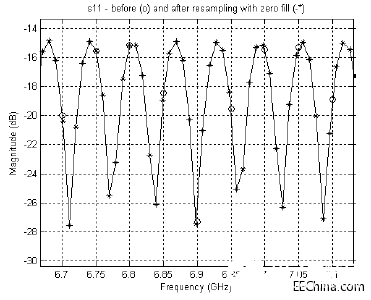
图10. 再采样前和再采样后s11放大的幅度响应。
四、最终结果
我们把上面介绍的插补和再采样算法应用到图5所示的3个S参数集中。现在组合S参数覆盖的总时间超过100 ns。我们对S参数再采样,间隔小于10MHz,直到25 GHz。图11显示了得到的时域图。t21和t11脉冲不再有假信号。现在t21脉冲位于正确的延迟位置,即23.9 ns。同样,t11反射位于正确的位置,即47.8 ns。较好的再采样选择一般是以更小的频率间隔重新测量数据。这是因为插补复杂的S参数数据有许多相关困难。但是,在重新测量数据不实用或不可行时,可以使用本文中介绍的算法。











