对于调制应用而言,涉及到频谱的搬移,因此采用双边带频谱更加方便。下文所涉及的频谱,均指双边带频谱。双边带频谱包括负频率成分,没有具体物理意义,但是从数学角度讲,这些又是构成傅里叶变换的必不可少的组成部分。
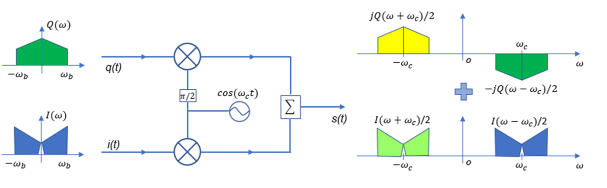
图2所示的IQ 调制器,在上变频的过程中,两个Mixer 实际上起到乘法器的作用,即i(t) 与cos(ωct )相乘,q(t) 与sin(ωct) 相乘,最后合为一路输出。
假设I(ω) 和Q(ω) 分别为i(t) 和q(t) 的傅里叶变换,而三角函数的傅里叶变换为
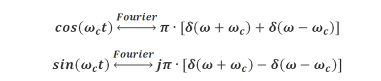
根据频域卷积定理可得:
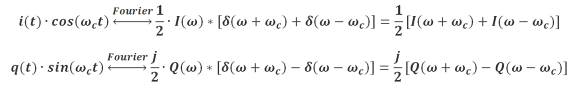
由此可见,i(t) 和q(t) 经过混频器后,从傅里叶的角度看,其双边带频谱发生了搬移,中心频率由DC 搬移至ωc。傅里叶变换的产物中还包含(-ωc)频率成分,如前所述,负频率不具有实际物理意义,但是作为傅里叶变换的重要组成部分,构成了整个变换的数学完整性。
虚数 j 的存在表明,两部分信号之间的载波存在90°相差,二者保持正交。
以上数学推导也可以由图解完成,图3给出了正、余弦函数的傅里叶变换示意图,模拟IQ 信号经过调制器后,频谱变换示意图如图4所示。
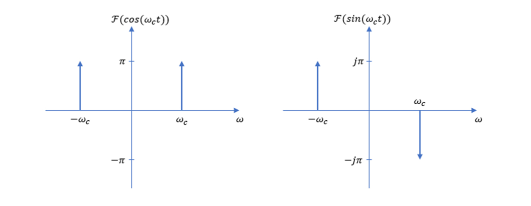
图3. 正、余弦三角函数的傅里叶变换