先分别通过一个古代的和一个现代的故事,看看 Shamir 秘密共享算法究竟是怎么回事吧。
这些故事的隐含前提是你对密码学有起码的了解,必要的话,你可以先温习一下 密码学与公钥基础设施引论。
一个古代关于加解密的故事
古代某国,国王有个大秘密,很大很大的秘密:
大到连他自己的孩子都不能轻易信任。他有五个子女,但他知道前路危机重重。他的孩子需要在他百年之后用这个秘密来保卫国家,而国王又不能忍受自己的孩子在他们还记得自己的时候就知道这些秘密,尤其是这种状态可能要持续几十年。
所以,国王动用大力魔术,将这个秘密分为了五个部分。他知道,可能有一两个孩子不会遵从他的遗嘱,但绝对不会同时有三个或三个以上会这样:
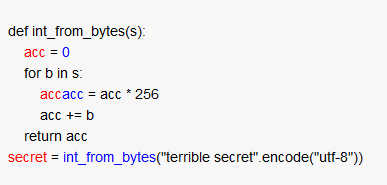
from mod import Mod
from os import urandom
国王精通 有限域 和 随机 魔法,当然,对他来说,使用巨蟒分割这个秘密也是小菜一碟。
第一步是选择一个大质数——第 13 个 梅森质数(2**521 - 1),他让人把这个数铸造在巨鼎上,摆放在大殿上:
P = 2**521 - 1
但这不是要保密的秘密:这只是 公开数据。
国王知道,如果 P 是一个质数,用 P 对数字取模,就形成了一个数学 场:在场中可以自由进行加、减、乘、除运算。当然,做除法运算时,除数不能为 0。
国王日理万机,方便起见,他在做模运算时使用了 PyPI 中的 mod 模块,这个模块实现了各种模数运算算法。
他确认过,自己的秘密比 P 要短:
secret < P











