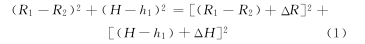
式中ΔH是单个铙钹的轴向变化量;ΔR为金属-陶瓷复合圆片的径向位移。忽略式中的高次因子ΔR2和ΔH 2,可得:
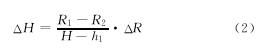
由于每个压电复合振子有两个铙拔结构,因此上述关系应乘以2。
鉴于国内的实际供货情况,选用厚度方向上极化的PZT5A型压电陶瓷圆片制作Cymbal型复合压电振子。压电振子的参数为:弹性柔顺常数sE11=16.4×10 -12(m2/N),泊松比μ0 ≈ 0.35,比重ρ0=7.75×10 3 (kg/m3),半径R0=10 mm,厚度h0=1 mm。铙钹是用厚度h1为0.3 mm的高弹性铍青铜(QBe1.9)带材冲压成型的,铙钹的有关参数为:弹性模量YE=135 Gpa,密度ρ1=8.29 g/cm3, 泊松比μ1=0.35,铙钹外缘半径R0=10 mm,内腔的底面半径R1=7.5 mm,顶面半径R2=2.5 mm,高度H=0.5 mm。最后,用AB环氧树脂胶把陶瓷圆片和上、下两铙钹的边缘粘接起来,即可制成Cymbal。整个压电陶瓷作动器由20枚复合压电振子在结构上串联粘接而成。将上述参数带入到(2)式,可得实际铙钹式压电作动器对于压电陶瓷片径向变形的放大倍数K=50。
1.3复合压电振子驱动特性
由于压电振子与铙钹粘在一起,这必然要对压电振子的机电特性产生影响。对于压电陶瓷薄片来讲,外加电场将会影响压电材料内部电偶极子排列的一致程度,而电偶极子的一致排列又会在压电材料的内部产生相应的感应电场,而其内部感应电场的强弱又反过来影响压电材料内部电偶极子排列的一致程度,如此循环往复直到平衡为止。对于Cymbal型复合压电振子来讲,当压电振子发生径向变形时,其必然要受到铙钹相反方向的约束力,而根据压电方程压电振子的受力又会反过来影响压电振子的形变,即压电振子的形变与其所受的约束力之间相互作用直到平衡为止。因而,复合压电振子的变形与外加电场之间呈现出非常复杂的关系。
图2为压电作动器的实测电压位移特性曲线图。
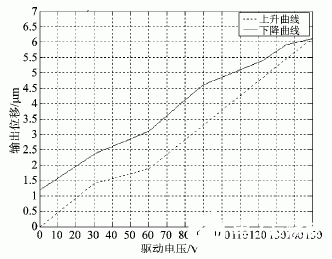
图2Cymbal型复合压电作动器实测电压位移特性曲线
2 控制系统设计
2.1系统组成
由于Cymbal型复合压电作动器的非线性与磁滞性,设计了如图3所示的闭环控制系统来实现作动器的微进给控制。











