其不等式约束条件为

式(3)(4)中:x C1(n)为n 次滤波支路的基波容抗;PC和PL分别为电容器和电感器单位容量的价格指标;QCZ和QLZ分别为滤波装置电容器总容量和电抗器总容量;Q b(n)为n次滤波支路基波无功功率的补偿容量;Q breq为系统所需的无功补偿容量。对图1 所示的5、7、11、13 次滤波支路(a相)进行综合补偿时,电容器组总的安装容量为:
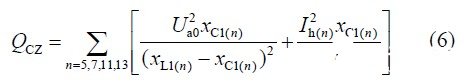
电抗器组总的安装容量为:
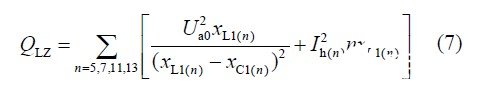
式(6)(7)中I h(n)为谐波电流。
2 新型换流变压器配套滤波装置的优化算法
在解决滤波装置的非线性规划问题时,通过构造合适的惩罚函数,可将有约束的优化问题转化为无约束的优化问题。本文定义的辅助函数为:
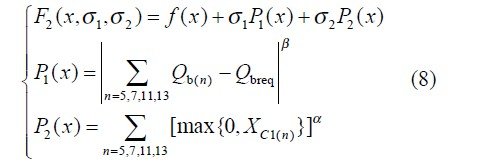
式中:σ 1和σ2 分别为对等式约束和不等式约束的惩罚因子;a为触发角;b 为换相角。当x为问题的可行点时,F(x,σ1,σ2 ) = f (x);当x不是问题的可行点时,σ1P1(x) +σ2P2 (x) 为很大的正数,可视为对x脱离可行域的一种惩罚,其作用是在极小化F2 (x,σ1,σ2 ) 的过程中迫使迭代点靠近原问题的可行域。因此求解式(6)即可得到式(3)的近似解,且s越大,近似程度越好。
采用遗传算法寻优时,本文充分利用外罚函数的特点,通过设置罚因子的步长pstep 对惩罚因子σ1 、σ2 作变量处理。在遗传算法的迭代过程中,通过评价每一代对约束条件的执行情况实施不同程度的惩罚,达到提高收敛性、获取全局最优解的目的。新型换流变压器配套滤波装置的优化算法流程图见图4。图中σ *1 和σ*2 为修正后的惩罚因子。
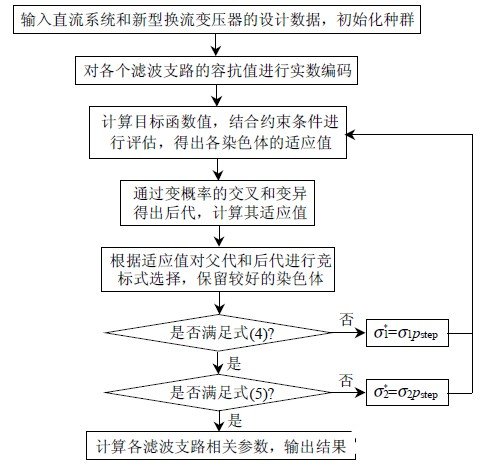
图4 新型换流变压器配套滤波装置的优化算法流程图
3 算例及仿真分析
以新型换流变压器直流输电模拟系统为研究对象,单极方式运行的12 脉动换流器的触发角a =15°,换相角b = 20°,直流侧输出电压为1000V,直流侧输出电流为100 A。新型单相换流变压器的额定容量为18.2294 kVA,一次侧额定电压U1=220V,一次侧额定电流I1=81.65A,一次侧等值电抗x1=0.4292 Ω;二次侧公共绕组额定电压U2=196.7025V,二次侧额定电流I2=47.14A,二次侧等值电抗x2=0.002 111 Ω;二次侧延边绕组额定电压U3=113.5662V,二次侧延边绕组额定电流I3=81.65 A,二次侧延边绕组等值电抗x3=0.1304 Ω。











