1.先要了解拉氏变换为什么会用在电路分析。拉氏变换在数学里可以用来间接地求解线性常系数微分方程(组),《现代控制理论》就是这应用。当然还有别的用处,比如概率论里“矩母函数”等等。在电路与系统中,动态电路(有电容电感的往往是这样)可以用线性常系数微分方程描述。请自行复习一阶二阶电路的时域求解。因此,从概念上讲,电路分析使用拉氏变换可以接受。

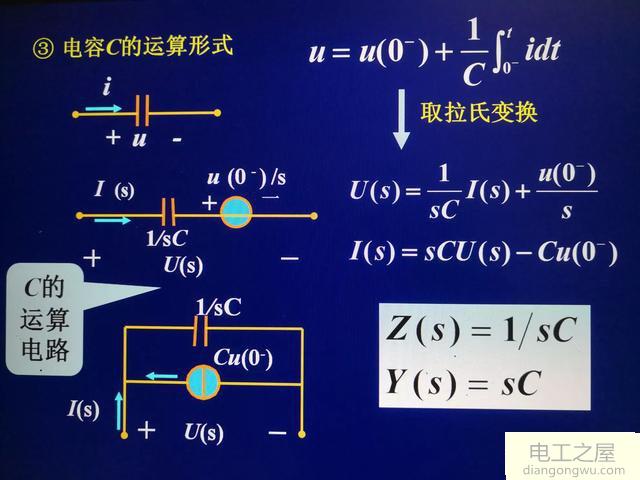
此图是西交邱关源课件,有错!这数学太烂了
2.一定要清楚,(集总参数)线性电路分析实际上是基尔霍夫定律和伏安关系(VCR)的综合应用。电路分析最给力的方法是回路法和节点法。其中需要两对概念自阻互阻,自导互导。求解电阻电路只要用观察法一下就能写出线性代数方程组。
动态电路必须服从基尔霍夫(KL)的约束,这不用强调。重要的是,动态元件L、C的VCR的时域形式是微积分。请立刻思考,节点法回路法为什么不能用在时域?
理由是,你说说,在时域内考虑,一个电阻串联一个电容,自阻或者互阻是什么?😂😂😂😂事实上,需要建立频域或者复频域的阻抗和导纳的概念。
请对比正弦稳态电路如何使用节点法和回路法。对,只要建立相量形式的KL和VCR。有了这个形式,称为相量模型,电阻电路的绝大多数分析法就直接推广到正弦稳态电路,比如阻抗串并联,节点法回路法,最大功率等等。但是相量法只能求出正弦稳态解,不能求出带有指数函数的暂态解。
不论稳态暂态,都是微分方程的解。然而,高阶电路列写微分方程求解都有困难,于是拉氏变换就登场了:间接求解。但不是先列写微分方程。
现在,虽然问题不再是仅仅求稳态解,但推广的思路与相量法完全一样。粗略说,只要建立运算模型,就是取拉氏变换后的KL和VCR。然后再反变换。
你明白了,拉氏变换比相量法用途更广泛。然而,处理正弦稳态毫无疑问都是相量法,所谓“因为相量法专注于正弦稳态,所以专业”😂。
3.好了,既然要对KL和VCR取拉氏变换,那么,对应的,拉氏变换的线性性质和微分性质是第一位重要的性质。因为KL就是电压(电流)加减法;LC的VCR是微(积)分。务必牢记。
4.要能熟练运用拉氏变换的微分性质推导L、C的运算模型,熟练作出其电路(串联形式)。不建议强背。

5.务必记住两条基本变换对。
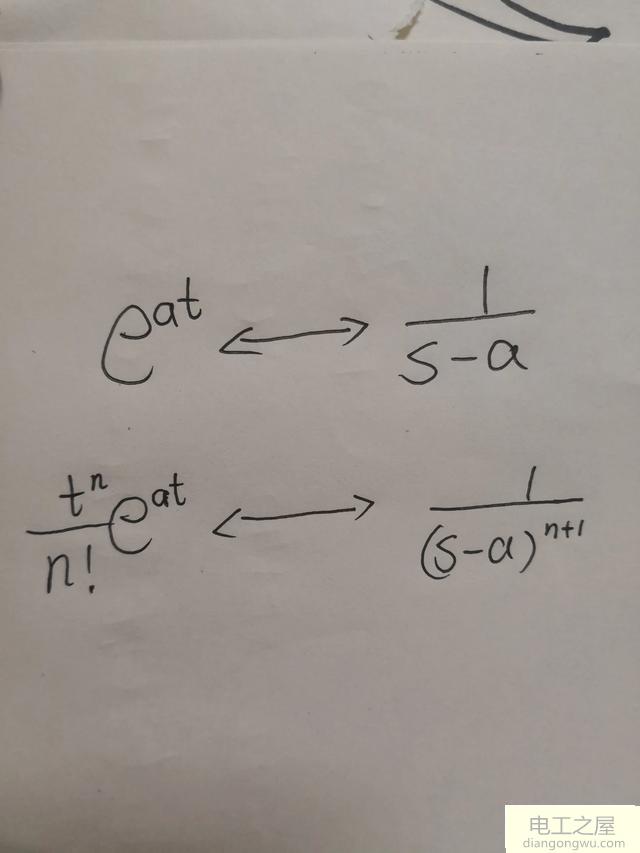
这两条是本质的。因为对应着微分方程的齐次通解:特征根互不相同,特征根有相同的重根。
记忆方法:第一条,“此根即彼根”。稍微解释一下。左边,微分方程的特征根就是指数里的a;右边,分母的根也是a。
第二条,左边指数函数的系数恰好是指数函数泰勒展开式第n项;右边分母是n+1次方。
6.熟记线性性质,微分性质,积分性质,特别是频移性质。大多数变换对都可以用基本变换对和四条性质推出来,对付考试足够。下面纯手写,推邱关源表14-1。

自己亲自推三遍就熟练了。
6.非常见函数拉氏变换与反变换。通通凑成基本变换对,或者指数乘以三角函数。反变换是重点,要会部分分式展开,也是凑。这个很容易,象函数的分母只有两种情况,单根,重根。(共轭复根看做单根,不要背公式,注意分子也共轭就行)
这个是纯微积分操作,非常容易。(用高数的思路,不必照电路课本的方法)自己亲自做邱关源例题14-6,14-7,14-8。
7.拉氏变换求解电路步骤
第一步,激励函数、LC取拉氏变换,作运算模型
第二步,按照节点法或者回路法,应用自(互)复阻抗的概念即可。列写S变量的方程(这是代数方程),
第三步,求解象函数
第四步,象函数取反变换。
找三四个题目做做。
最后,用拉氏变换可以定义网络函数,就是信号与系统和自控原理的传递函数,拉氏变换的威力就进一步展现出来了。











