rlc串联电路关系式和矢量图
1.瞬时值关系式:和上面的电路一样,它也符合克希荷夫电压定律。
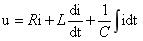
2.有效值关系:这个公式和上面的一样,也是通过矢量图推算出来的,由于电容、电感的相位相反,因此为相减关系。这正是这个电路的特色之处,得到了非常广泛的应用。从公式上看三者串联之后比单一的L或者C的电流要大。因为电容和电感相抵消了一部分或者全部。

3.阻抗:从公式上看,这种电路的阻抗比单一的电感L或者电容C要小,电容和电感相抵消了一部分或者全部。

4.矢量图:从图上可以看出加在电感、电容上的电压相位是相反的,它们大小可以一样,可以不同,因此整个电路可以是阻性,可以是容性,也可以说感性的。这一切取决于电路的参数。
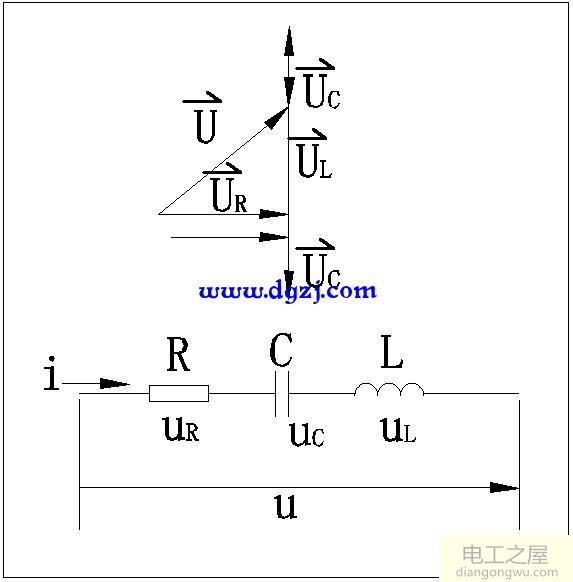
5.功率,视在功率S=UI,有功功率P=UIcosα,无功功率Q=UIsinα,且三者关系为:
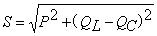
6.功率因数:
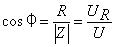
应用:从阻抗关系可以看出,RLC可以组成容性、感性、阻性电路,取决于L、C、f参数关系;其中电阻性关系可以组成谐振电路,也就是非常有名的LC串联谐振电路,谐振时电路阻抗最小,为纯电阻,电流最大,支路电压可以远大于总电压。正是这个特点在选频电路中得到了广泛的应用。如下图中直放式收音机的输入谐振电路就是典型的LC串联谐振电路。
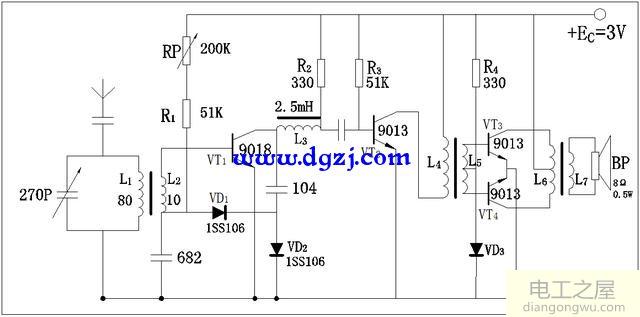
直放式收音机电路图











