PID算法及参数整定方法
1.位置表达式
位置式表达式是指任一时刻PID控制器输出的调节量的表达式。
PID控制的表达式为
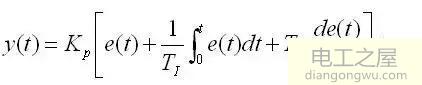
式中的y(t)为时刻t控制器输出的控制量,式中的y(0)为被控制量没有偏差时控制器输出的控制量。
由于计算机进入了控制领域。人们将模拟PID控制规律引入到计算机中来。由于计算机控制是一种采样控制,它只能根据采样许可的偏差计算控制量,而不能象模拟控制那样连续输出控制量,进行连续控制。由于这一特点,上面公式中的积分和微分项不能直接使用,必须进行离散化处理。离散化处理的方法为:以T作为采样周期,k作为采样序号,则离散采样时间kT对应着连续时间 t,用求和的形式代替积分,用增量的形式代替微分,可作如下近似变换:

上式中,为了表示方便,将类似于e(kT)简化成 ek 形式就可以得到离散的PID表达式:
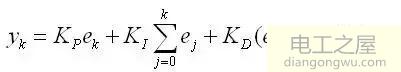
或写成
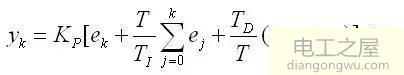
此公式即为位置式的PID表达式。
式中:k ——采样序号,k=0,1,2,…
yk ——第k 次采样时刻的计算机输出值
e k ——第k 次采样时刻输入的偏差值
e k −1 ——第k-1 次采样时刻输入的偏差值
K I ——积分系数。K I = KP*T/TI
积分时间TI即为累积多少次/个T)
KD ——微分系数。K D = KP*TD /T
如果采样周期取得足够小,则以上近似计算可获得足够精确的结果,离散控制过程与连续控制过程十分接近。
2.增量式表达式
利用上面的公式,可得出第k次采样、第k-1次采样时的输出调节量yk、yk-1,用yk-yk-1,即得增量式PID表达式,如下:
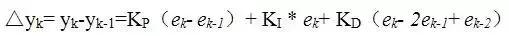
在实践中,把具体整定的方法总结了几段顺口溜:
参数整定找最佳,从大到小顺次查,
先是比例后积分,最后才把微分加;
曲线振荡很频繁,比例度值要放大, //比例度放大即比例系数KP要减小。
曲线漂浮绕大弯,比例度值应减小;
曲线偏离回复慢,积分时间往下降,
曲线振荡周期长,积分时间再加长;
曲线振荡频率快,先把微分降下来,
动差大来波动慢,微分时间应加长;
理想曲线两个波,前高后低四比一,
一看二调多分析,调节质量不会低。
第一段讲的是整定顺序,δ和Ti都是从大到小逐步加上去,微分是最后才考虑的。第二段讲的是比例度如何整定。第三段讲的是积分时间如何整定。第四段讲的是微分时间如何整定。第五段讲的是标准。
上面这种方法步骤是先加δ,再加Ti,最后才加Td。应用中较稳妥。
另一种方法是先从表列范围内取Ti的某个数值,如果需要微分,则取Td=(1/3~1/4)Ti,然后对δ进行试凑,也能较快地达到要求。











