一阶RC低通滤波曲线特性图
典型电路
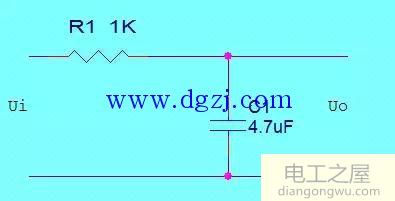
图1 典型RC电路
直流、交流、脉冲信号都可以用它
时域
电容电流:
Ic=dqdt=d(C∙Uo)dt=CdUodt
基尔霍夫电压定律得:
Ui=RCdUodt+Uo
Ui的单位是伏特,RC的单位为秒,τ=RC;
解得:
Uo(t)=Ui(1−e∧(−t/RC))
假设电容初始电压值为0
R=1000Ω
C=4.7uF
Ui=1V
t=0.0001~0.1s
τ=RC
Vc(τ)=0.632
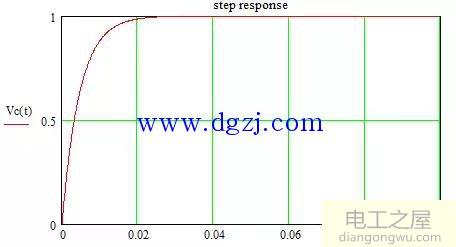
图2 一阶RC系统的阶跃响应曲线
频域
u1=Ui;u2=Uo;
以电容电压作为输出,电路的网络函数为:
H(jω)=U2U1=1jωCR+1jωC=11+jωRC
令ωc=
1RC=1τ
ωc即为截止频率;
幅值和相角函数:
|H(jω)|=11+(ωωc)2−−−−−−−−√
θ(ω)=−arctanωωc
各变量取值:
R=1000Ω
C=4.7uF
j=−1−−−√
ω=1RC
fc=12πRC
A(f)=1j2πfRC+1
|A(fc)|=0.707
θ(f)=180arg(A(f))π
θ(fc)=-45
f=0.001、1、…….100000
幅频和相频特性图:
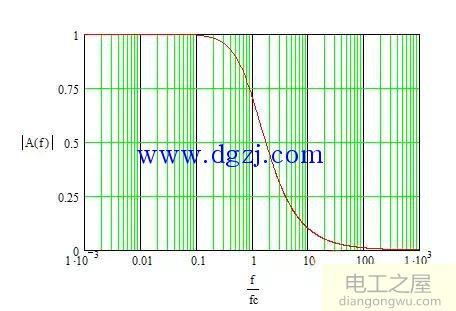
图3
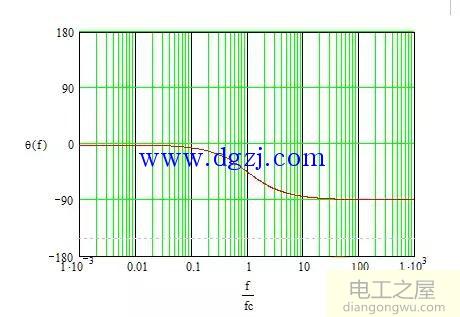
图4
幅频特性图的对数表示:
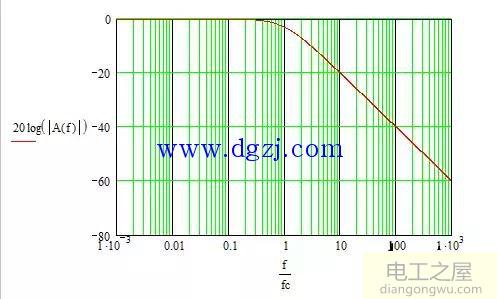
图5
-当ω
-当ω>>ωc时,是斜率与-20dB/十倍频成比例的一条直线;
-当ω=ωc时,增益衰减至0.707,即-3dB,相位滞后45度,对应低通滤波器,该频率通常被称为截止频率。
缺点:
采用这种模拟滤波器抑制低频干扰时,要求滤波器有较大的时间常数和高精度的RC网络,增大时间常数要求增大R值,其漏电流也随之增大,从而降低了滤波效果;
软件上的一阶低通滤波
优点:
-采用数字滤波算法来实现动态的RC滤波,则能很好的克服模拟滤波器的缺点;
-在模拟常数要求较大的场合这种算法显得更为实用;
-其对于周期干扰有良好的抑制作用,
-比较节省RAM空间
缺点
-不足之处是带来了相位滞后,导致灵敏度低;
-同时它不能滤除频率高于采样频率的二分之一(称为奈奎斯特频率)的干扰(例如采样频率为100Hz,则它不能滤除50Hz以上的干扰信号)对于高于奈奎斯特频率的干扰信号,应该采用模拟滤波器。
-对没有乘、除法运算指令的单片机来说,程序运算工作量较大











