动态电路的方程
分析动态电路,首先要建立描述电路的方程。动态电路方程的建立包括两部分内容:一是应用基尔霍夫定律,二是应用电感和电容的微分或积分的基本特性关系式。下面通过例题给出详细的说明。
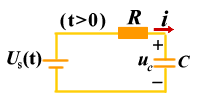
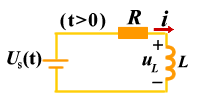
图 4
图5设 RC 电路如图4 所示,根据 KVL 列出回路方程为:
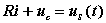
由于电容的 VCR 为:
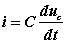
从以上两式中消去电流得以电容电压为变量的电路方程:
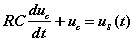
若以电流为变量,则有:
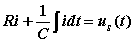
对以上方程求导得:
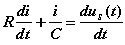
设 RL 电路如图5 所示的,根据 KVL 列出回路方程为:
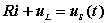
由于电感的 VCR 为:
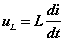
以上两式中消去电感电压得以电流为变量的电路方程:
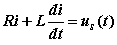
若以电感电压为变量,则有:
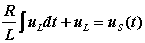
对以上方程求导得:
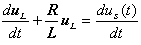
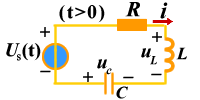
对图6 所示的 RLC 电路,根据 KVL 和电容、电感的 VCR 可得方程为:
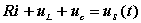
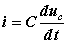
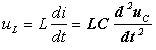
图6整理以上各式得以电容电压为变量的二阶微分方程:
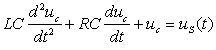
考察上述方程可得以下结论:
(1)描述动态电路的电路方程为微分方程;
(2)动态电路方程的阶数等于电路中动态元件的个数,一般而言,若电路中含有 n 个独立的动态元件,那么描述该电路的微分方程是 n 阶的,称为 n 阶电路;
(3)描述动态电路的微分方程的一般形式为:
描述一阶电路的方程是一阶线性微分方程
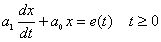
描述二阶电路的方程是二阶线性微分方程
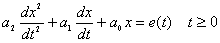
高阶电路的方程是高阶微分方程:
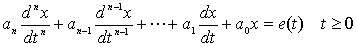
方程中的系数与动态电路的结构和元件参数有关。
3. 电路初始条件的确定
求解微分方程时,解答中的常数需要根据初始条件来确定。由于电路中常以电容电压或电感电流作为变量,因此,相应的微分方程的初始条件为电容电压或电感电流的初始值。
若把电路发生换路的时刻记为 t =0 时刻,换路前一瞬间记为0-,换路后一瞬间记为0+,则初始条件为t=0+时u ,i 及其各阶导数的值。
(1)电容电压和电感电流的初始条件
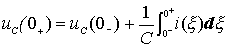
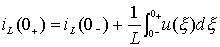
由于电容电压和电感电流是时间的连续函数(参见第一章),所以上两式中的积分项为零,从而有:
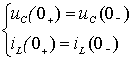
对应于
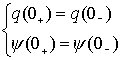
以上式子称为换路定律,它表明:
1) 换路瞬间,若电容电流保持为有限值,则电容电压(电荷)在换路前后保持不变,这是电荷守恒定律的体现。
2)换路瞬间,若电感电压保持为有限值,则电感电流(磁链)在换路前后保持不变。这是磁链守恒的体现。
需要明确的是:
1)电容电流和电感电压为有限值是换路定律成立的条件。
2)换路定律反映了能量不能跃变的事实。
(2)电路初始值的确定
根据换路定律可以由电路的uC(0-) 和iL(0-) 确定uC(0+)和iL(0+) 时刻的值 , 电路中其他电流和电压在 t=0+ 时刻的值可以通过 0+ 等效电路求得。求初始值的具体步骤是:
1)由换路前 t=0-时刻的电路(一般为稳定状态)求uC (0-) 或 iL (0-) ;
2)由换路定律得uC (0+) 和iL (0+) ;
3)画 t=0+ 时刻的等效电路: 电容用电压源替代,电感用电流源替代(取 0+ 时刻值,方向与原假定的电容电压、电感电流方向相同);
4)由 0+ 电路求所需各变量的 0+ 值。











