传递函数转换差分方程 开环传递函数

如何把传递函数转换为差分方程,为了整个推导过程，我们先分析积分环节1/s，

假设这个积分环节的输入时误差信号E(s),输出为Y(S),则传递函数的表达式 Y(s)/E(s)=1/s,或者Y(s)=E(s)/s

这样表达式在几何上的意义入下图:

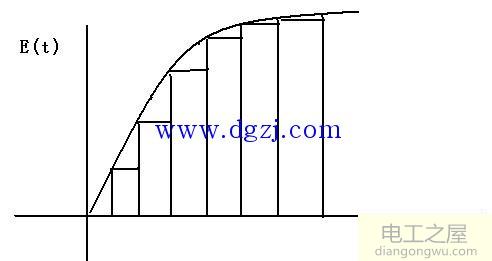
Y(t)为E(t)的积分，也就是E(t)曲线下的面积。对于这样的面积，一个简单的推导公式就可以列出来了。控制周期为Tc.

如果最简单的矩形表示

Y(t):=Y(t-1) + E(t)*Tc

如果用稍微复杂一点表示，就是用梯形的面积来进行近似

Y(t):=Y(t-1) + (E(t)+E(t-1))*Tc/2

上面两个差分方程用Z变换写出来,

Y(Z):= Z-1 Y(Z)+E(Z)*Tc => Y(Z)/E(Z)= Tc * (1/(1-Z-1 ))

Y(Z):= Z-1 Y(Z)+(E(Z)+E(Z)*Z-1 )*Tc/2 => Y(Z)/E(Z)= Tc/2 * (1+Z-1 )/(1-Z-1 ))

在拉普拉斯变换中 Y(s)/E(s)= 1/s;

这样我们就得到了S 变换和Z变换的关系

1/S = Tc * (1/(1-Z-1 )) 或者

1/S =Tc/2 * (1+Z-1 )/(1-Z-1 ))

这样对于任何一个拉普拉斯表达式，只要按照上面的公式将S表达式换成Z表达式，再把Z变换写成差分方程，

有了差分方程，那么恭喜你，可以写程序了。