什么是绝对值数字编码?

以传感器内部信号获得的有和无,电学的高低电平作为 1 和 0 的编码,有 N 位的 0、1 编码(也称为二进制编码)组成的绝对值编码。数字式编码的有和无,对于各种微动因素的干扰引起的大小变化不敏感,为此抗干扰性强。目前越来越多的应用采用绝对值编码器。
绝对值数字编码的方式有哪些?
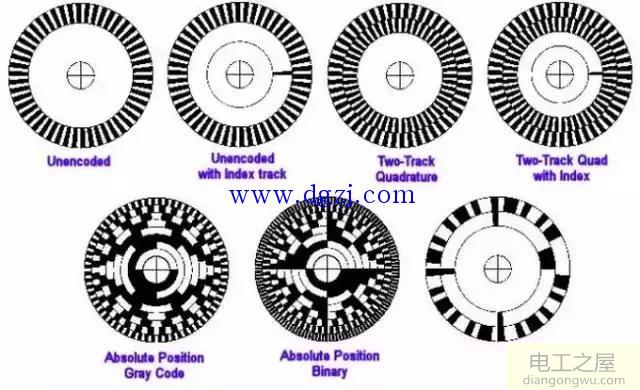
十进制码
日常生活中,我们的数字是 0~9,逢十进一,这称为“十进制”数字编码;
因 10 进制编码需要用十个阶梯的分布物理量,物理实现较不方便,编码器中很少用此编码。
纯二进制码
现代电子数字编码,一般都以通断(明暗)代表 0、1,有多位数 2 的 N 次方构成编码,最简单的就是纯二进制编码 BIN,变化的数字就是 0 和 1,逢二进一,这称为“纯二进制”数字编码,计算机电子应用中较多以此为编码。
16 进制码
以二进制 4 位一组向十进制解码 0~15,但是 10 以上不以两位数表示,而是以 A~F 表示,如 10 为 A,15 为 F,这是 16 进制的编码,便于数据寄存及辨识。
BCD 码
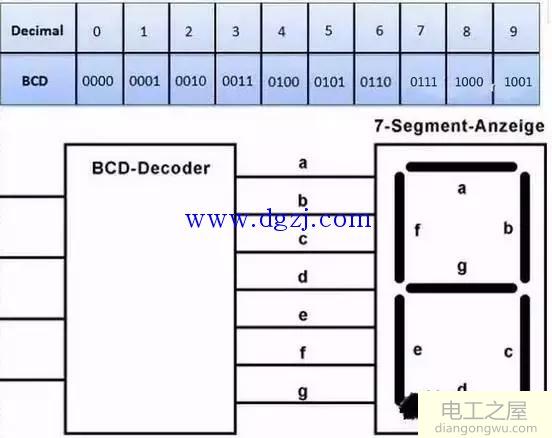
十进制每一位分解解码到二进制码的4位一组十个数,其 BCD 码向十进制解码后只有 0~9,而无需再考虑十进制的进位问题,一般用于人眼习惯的 7 段数码显示管。
格雷码

格雷码是二进制编码的一种,其特征是每一次递增(或递减)一个字变化,所有位数上只有其中一位发生了改变(0 与 1 的变化),并且数据终点循环到起点同样遵循这个原则,这样在一个字的变化过程中,只有一位数发生跳变,数“能”变化量最小,出错概率最低。特别适合于绝对值编码器的多码道同步读取或多位数同步输出(并行输出)中,也适合在通讯传输中。
格雷余码
二进制编码中大部分是 2 的幂次方编码,编码总数也是 2 的幂次方,如 8 位的 256、10 位的 1024 等,在编码器的角度计算中,在角度计算中无法整除取整,有时要用到角度的整数,为此有格雷余码,在格雷码的数码中去除一部分,余下一部分编码使用,因此也称为“余格雷码”,例如 180、360、720 个编码的“余格雷码”。格雷余码向十进制解码后的十进制数不从 0 开始,需要“补码”。
其他编码
在通讯传输中,还有一些不常见的编码,是上述编码形式的变异或组合,例如曼切斯特编码等,这里就不一一叙述了。











