积分电路和微分电路在波形产生及变换电路中用的很广,简单的积分电路和微分电路只有一个电阻和电容即可构成。下面我们来介绍一下积分电路和微分电路的基本工作原理及用途。
1、积分电路
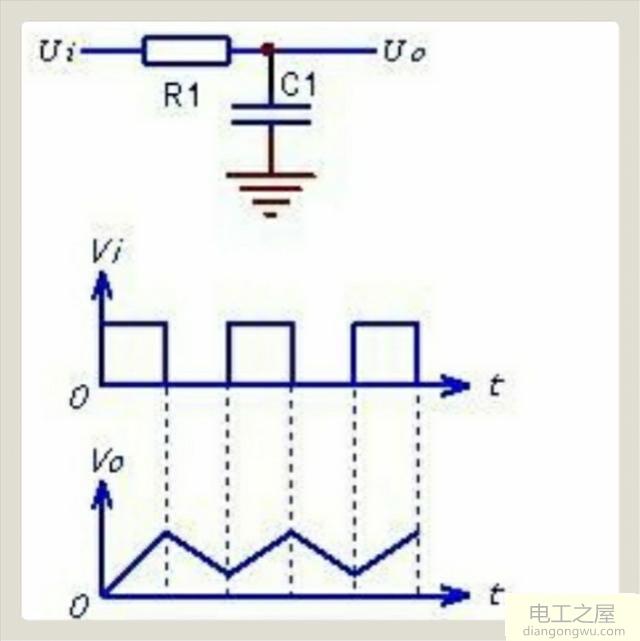
积分电路及波形图。
上图是一个采用电阻和电容构成的简单的积分电路,其在各种波形变换电路中用的很广,该电路可以将输入端的方波信号(可由方波发生器产生)转为三角波或斜波并从电容C1两端输出。积分电路的积分时间常数τ=R1C1,R1和C1的取值很重要,一般只有在积分时间常数τ≥10倍输入脉冲宽度时上述的阻容电路才是积分电路,才可以实现积分功能。
上图中,假设输入信号为方波,并且积分时间常数大于输入脉冲宽度,在方波信号的正半周时,通过R1对C1充电,C1两端的电压逐渐增大;输入方波的负半周时,C1通过R1放电,C1两端电压又开始下降,波形如上图所示。上述这种简单的积分电路只在充电曲线的初始部分,输出电压与输入波形的时间间隔成线性关系,随着时间的增加,积分误差将逐渐增大,故一些要求较高的积分电路常采用运算放大器来设计。
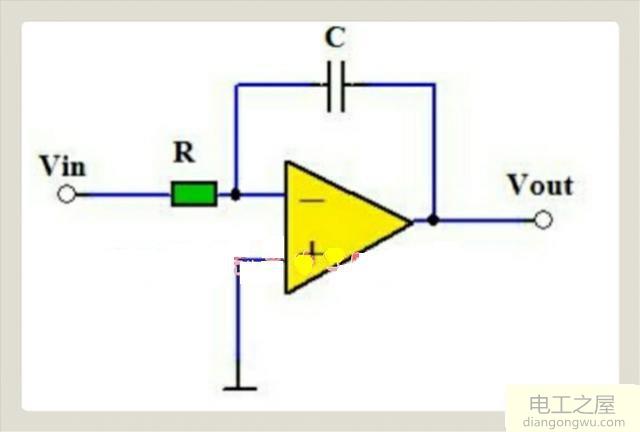
运算放大器构成的积分电路。
上图所示的积分电路采用运算放大器设计,其积分运算精度及带负载能力皆显著优于阻容分立元件构成的积分电路。
2、微分电路
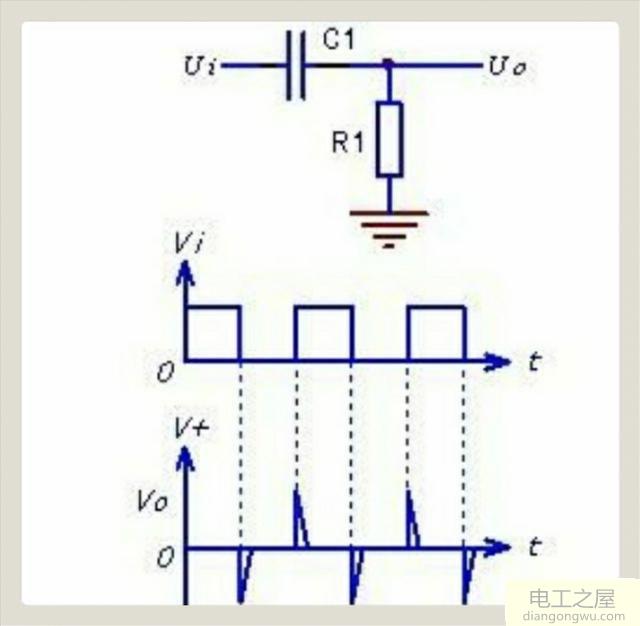
微分电路及波形图。
微分是积分的逆运算,故将积分电路中的电阻和电容位置调换一下即可构成微分电路。阻容微分电路看起来与阻容耦合电路差不多,它们的区别就是电阻和电容的取值不同。只有微分时间常数τ≤10倍输入脉冲宽度时,这种阻容电路才是微分电路。若电路的时间常数远大于输入脉冲宽度,电路将成为阻容耦合电路。
微分电路可以将方波信号转为尖脉冲(微分电路的输出波形如上图所示),这在各种脉冲触发及控制电路中很常用。譬如数字电路中各种触发器的触发与复位,就经常采用这种简单的阻容微分电路来产生正负触发脉冲。











