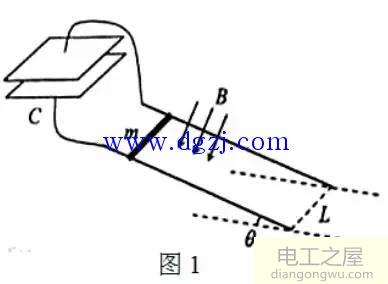
例题:如图1所示,两条平行导轨所在平面与水平地面的夹角为θ,间距为L。导轨上端接有一平行板电容器,电容为C。导轨处于匀强磁场中,磁感应强度大小为B,方向垂直于导轨平面。在导轨上放置一质量为m的金属棒,棒可沿导轨下滑,且在下滑过程中保持与导轨垂直并良好接触。已知金属棒与导轨之间的动摩擦因数为μ,重力加速度大小为g。忽略所有电阻。让金属棒从导轨上端由静止开始下滑,求:
(1)电容器极板上积累的电荷量与金属棒速度大小的关系;
(2)金属棒的速度大小随时间变化的关系。
分析:
金属棒由静止释放瞬间计为t=0时刻,将立体图转化为平面图,对金属棒受力分析如图2所示:
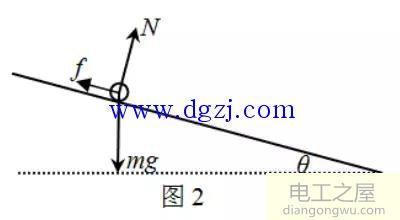
根据题意金属棒从导轨上端由静止开始下滑可知:
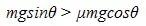
金属棒将沿着导轨向下加速下滑,切割磁感线,产生感应电动势,相当于一个电源,电源对电容器充电,电容器两端的电压等于电源的电动势,设t时刻,金属棒的速度为v,根据电容器的电容定义式和动生电动势的表达式,不难写出第(1)问中电容器极板上积累的电荷量与金属棒速度大小的关系。
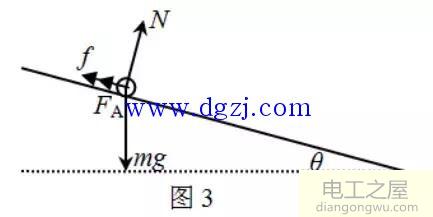
根据楞次定律可以判断出t时刻感应电流方向,根据左手定则可以判断出此时金属棒还受到沿着导轨向上的安培力FA,受力情况如图3所示。要研究金属棒的速度大小随时间变化的关系,需要研究金属棒的加速度情况,根据牛顿第二定律不难写出加速度的表达式,进一步判断金属棒的运动情况。
求解:



拓展1:
如图4所示,两条平行导轨固定在水平面上,间距为L,导轨左端接有一平行板电容器,电容为C。导轨处于竖直向下的匀强磁场中,磁感应强度大小为B。在导轨上放置一质量为m的金属棒,在水平恒力F的作用下,由静止开始沿着导轨向右滑动,滑动过程中保持与导轨垂直并良好接触。已知金属棒与导轨之间的动摩擦因数为μ,重力加速度大小为g。忽略所有电阻,求:
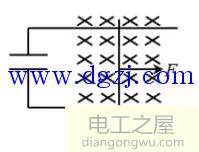
(1)电容器极板上积累的电荷量与金属棒速度大小的关系;
(2)金属棒的速度大小随时间变化的关系。
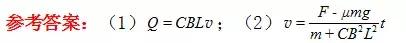
拓展2:
如图5所示,两根竖直放置与地面绝缘的金属导轨,间距为L,处于与导轨垂直的匀强磁场中,磁感应强度大小为B。导轨上端接有一平行板电容器,电容为C。导轨上有一质量为m的金属棒平行于地面放置,与导轨接触良好且无摩擦。开始时电容器不带电,由静止释放金属棒,忽略所有电阻,重力加速度大小为g,求:
(1)电容器极板上积累的电荷量与金属棒速度大小的关系;
(2)金属棒的速度大小随时间变化的关系。
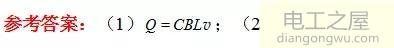
总结:
由例题、拓展1和拓展2可以看出在含电容器的闭合电路中,由恒力驱动切割磁感线的金属棒做匀变速直线运动,在例题中恒力可以认为是
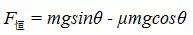
,
在拓展1中恒力可以认为是
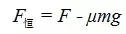
,
在拓展2中恒力可以认为是
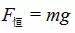
。
在运动过程中,金属棒相当于一个电源,对电容器进行充电,电容器极板上积累的电荷量与金属棒速度大小的关系都可以根据电容器的电容定义式和动生电动势的表达式写出,均为
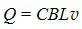
;金属棒的加速度可以通过对金属棒受力分析,根据牛顿第二定律写出,均为
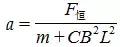
,不难看出加速度为一个定值,证实金属棒做匀变速直线运动。再结合运动学公式可以得到速度大小随时间变化的关系

。