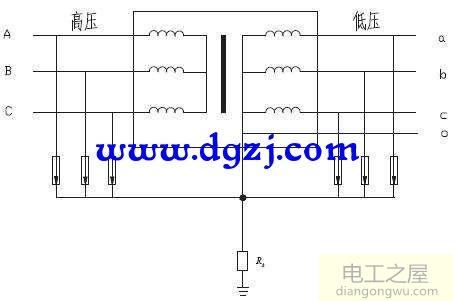
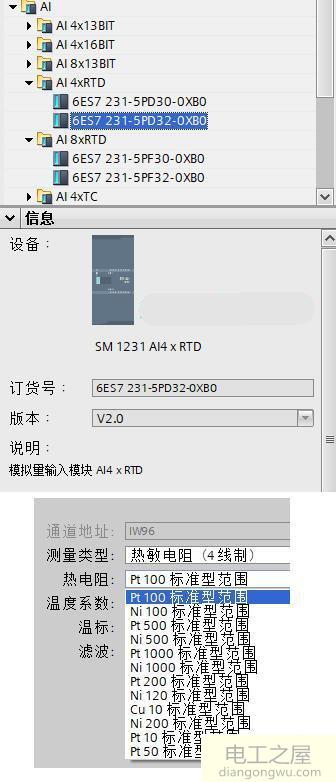
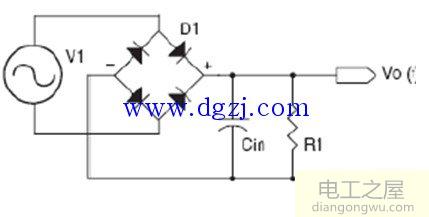
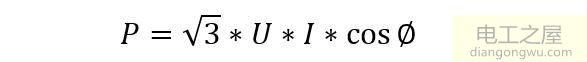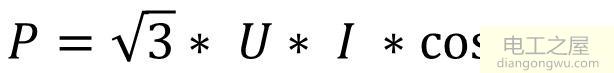测量相对误差计算公式
绝对误差是既指明误差的大小,又指明其正负方向,以同一单位量纲反映测量结果偏离真值大小的值,它确切地表示了偏离真值的实际大小。
相对误差是指“测量的绝对误差与被测量的真值之比”,即该误差相当于测量的绝对误差占真值(或给出值)的百分比或用数量级表示,它是一个无量纲的值。有的计量器具从实际使用的需要出发,为了确定其准确度或允许误差,往往用引用误差和分贝误差来表示。
引用误差是指绝对误差与特定值(测量范围上限值或量程)之比,值以百分数表示,它是相对误差的另一种表达形式。
分贝误差是无线电、声学等计量器具中经常用来表示相对误差的一种表达形式。将上述归纳起来就是相对误差的类别:
①实际相对误差;
②给出值相对误差;
③引用误差;
④分贝误差。
相对误差公式
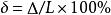
(δ—实际相对误差,一般用百分数给出,△—绝对误差,L—真值 )
相对误差原理
测量所造成的绝对误差与被测量〔约定〕真值之比。乘以100%所得的数值,以百分数表示。
约定真值:对于硬度等量,则用其约定参考标尺上的值作为约定真值。
实际相对误差定义式为
δ=△/Lx100%
式中:δ—实际相对误差,一般用百分数给出
△—绝对误差
L—真值
一个近似数与它准确数的差的绝对值叫这个近似数的绝对误差。用a表示近似数,A表示它的准确数,那么近似数a的相对误差就是|a-A|/A。
另外,由于测量值的真值是不可知的,因此其相对误差也是无法准确获知的,我们提到相对误差时,指的一般是相对误差限,即相对误差可能取得的最大值(上限)。
测量值的测量误差的绝对值与相应测量值的比值。为量纲为一的量,通常用分子为1的分数表示,常用于描述线量的精度。在描述线量(长度或仅与长度有关的物理量,如长度、面积、体积等)的精度时,既要考虑线量的误差的大小,还应顾及线量本身的大小。
例如,测量者用同一把尺子测量长度为1厘米和10厘米的物体,它们的测量值的绝对误差显然是相同的,但是相对误差前者比后者大了一个数量级,表明后者测量值更为可信。
指绝对误差在真实值中所占的百分率