分析思想就是通过模似随机抽样,对抽样的结果进行统计分析来作电路的容差计算。
下面就详细介绍一下用EXCEL来做此分析的具体操作步骤,通过这步步的介绍,相信你会对蒙特卡罗分析电路容差有清楚的了解。
为了好理解,我们以最简单的分压电路来作说明,电路描述如下:
分压电路的电源是VCC,标称值为5V,精度为2%,即公差为0.1V
分压电阻R1为100K,精度为1%,即公差为1K,该电阻一端与VCC相连
分压电路R2为100K,精度为1%,即公差为1K,访电阻的一端与R1相连,另一端与GND相连
因此,该电路的输出电压表达式为Uo = VCC*R2/(R2+R1)
第一步:蒙特卡罗分析首先就是要建议以上这个输出电压Uo的表达式;
第二步:对表达式中各参数按实际的分布进行随机抽样;我认为该分析中这一步很关键,那么在EXCEL中如何具体操作呢?在具体操作前,我想还需要再对上文中“按实际的分布”再作一下说明,不然理解起来可能有困难。
比如电阻,我们选的这两个都是100K,精度为1%的,我们需要对此深究一下这里面的具体意义。100K是电阻的标称值,就是说这种电阻值是100K左右,如果你买了一盘这种电阻,去测量每一个电阻的话不可能都是标准的100K,有些可能是100.4K,有些可能是99.8K等,总之这些电阻是在100K+-1%的范围内,基本上其平均值为100K,且大量个体的分布服从正态分布,且正态分布的两个参数分别是:均值μ为标称值,方差σ为公差的三分之一。
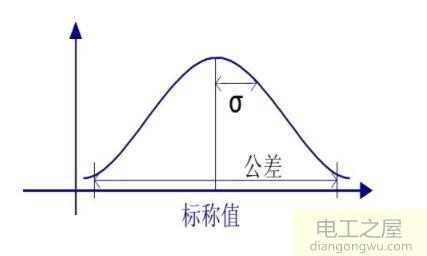
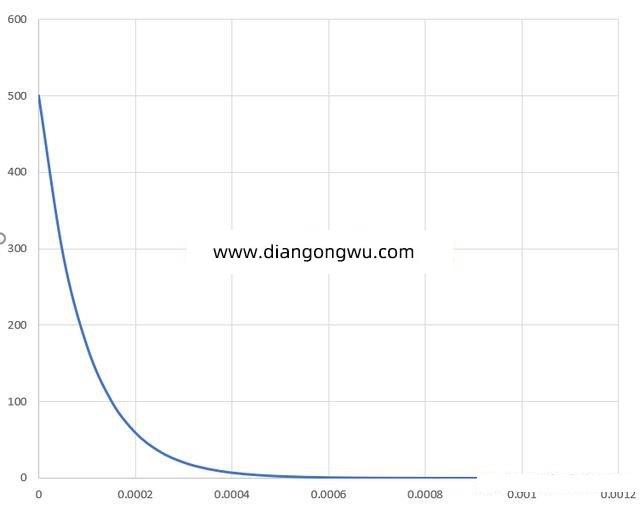
所以上文中说的按实际的分布进行随机抽样的意思就是按上图的概率分布进行抽样,抽样抽到标称值的机率最大,离标称值越远的值抽到的机率就越小。而EXCEL中就有这个函数可以很方便的按所需的分布类型来作随机抽样。具体的函数是NORMINV()和RAND(),按正态分布抽样的具体函数是NORMINV(RAND(),μ,公差/3),这样的话就可以得到一组随机抽样的参数R1, R2, VCC
第三步:将第二步中提到的一组随机抽样参数R1, R2, VCC代入输出电压表达式中,就可以计算出一个根据随机抽样参数得到的输出电压值。
第四步:反复进行第二步、第三步,这样的话就可以得到N组输出电压值
第五步:对这N组输出电压值进行统计分析,就可以得到相应电路的容差。
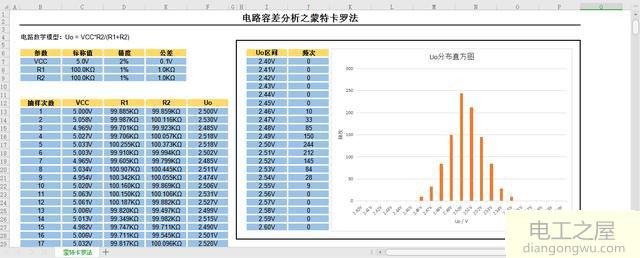
下图即是我用EXCEL对该电路做的一张蒙特卡罗容差分析法表格