模拟退火算法有可能摆脱局部最优,找到全局最优解,保证算法收敛。但是它只是搜索解空间中的一点且对解空间中已知试探的区域知之甚少,因此难以判断哪些区域有更多的机会找到最优解。所以,其收敛到全局最优解是非常耗时的。
1.3 模拟退火遗传算法
鉴于遗传算法的并行性和它在算法结构上的特点, 可以很容易地将遗传算法和其他算法混合使用, 从而达到扬长避短的作用。从上文的论述中可以看出,若将遗传算法的全局搜索功能和模拟退火的局部搜索功能互相补充,将相得益彰。
本文在遗传算法中融入模拟退火思想,首先,在选择操作中引入退火思想并允许适应度高的少量父代与子代共同竞争;其次,根据模拟退火思想设计出自适应交叉概率和变异概率,从而保证了种群的多样性以及收敛速度。模拟退火遗传算法的流程如下:
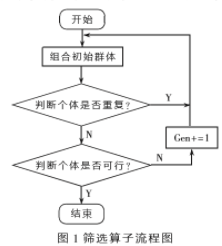
(1)初始群体的产生:为了得到理想的初始种群,首先在每个变量的取值范围内均匀产生种群,然后通过设计重组与筛选算子进行重新组合,从而保证其多样性和组合随机性。在经过交叉变异产生的子代中同样采用筛选算子使新一代种群中避免出现大量重复个体,使算法能够趋于收敛。筛选算子流程如图1所示。
(2)退火选择操作:运用适者生存法则,繁殖操作在旧的群体中“随机”选择符号串生成一个新的种群,但选择并非完全随机,它基于一个符号串相对于整个群体的适应度。在常用的轮盘赌选择方法中,个体被选中的概率遵循Montecarlo方法,与其适应度和种群的平均适应度的比值成正比:











