
式中:Δf为频率差;Δφ为相位差;f正、f逆为超声波在流体中顺流和逆流的传播频率;f为超声波的频率。
从中可以看出,相位差法本质上和时差法是相同的,而频率与时间又互为倒数关系,三种方法没有本质的区别。
普通方法测量时间差
所存在问题分析
从上述公式的推导中可以看出,要运用传播时间测流量时,最关键的测量量就是顺逆流传播时间差,只有精确得到这个时间差,流量才能由其导出。
对于小口径、低流速的情况,顺逆流的时差非常短,典型最大流量对应的时差仅约20ns,精确测量难度很大,需要极高的时钟频率。如果测量方法粗放,这个极小的时间量很可能被淹没在测量的误差中。因此,如何才能测量到这个时间量,并使其尽可能精确,就是本文要研究的环鸣法的关键所在。
环鸣法的设计确定
环鸣法的产生
为了解决时间差值太小的的问题,环鸣法利用了让小的量不断积累,使总体值增大,得到总量后再做平均的思想。环鸣法总方框图如图2所示。
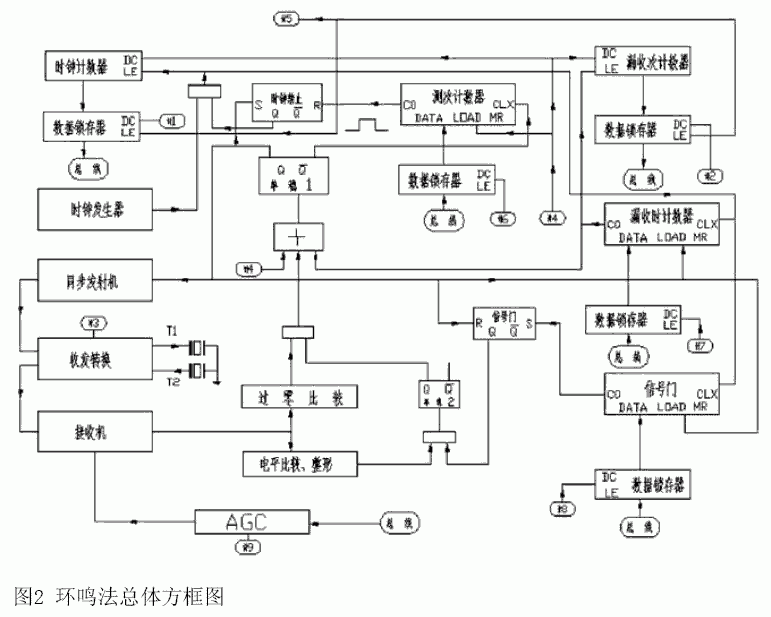
该方法中,当换能器T1发射声信号,在换能器T2收到信号的时刻,令T1再次发射声信号,而T2再次接收,这样如此循环发射、接收N次。通过测量记录下N次测量的总时间∑t正。然后,再令T2发射,T1接收,经过N次如此循环就可得到逆向发射总时间∑t逆。这时让顺逆流两个总的时间作差,可以得到总时间差∑Δt。∑Δt这个量比起单次测量时,它已经扩大了2N倍。由测量带来的误差经过了N次累加后,其均值则向零靠近,使得测量精度提高了倍。此时这个值就较容易测量,从而得到想要的流量数据。











