图3 ( a ) 悬臂梁在9 V驱动电压下的Z向位移图(l=300 μm,t=2 μm,g0=2 μm);一字型悬臂梁驱动电压的理论计算和仿真数值对比图,(b) 当l为变量,(t=2 μm、g0=2 μm);图(c) t为变量,(l=300 μm、g0=2μm);(d) g0为变量,(l=300 μm、t=2 μm)。
针对一字型悬臂梁模型进行了改进,分别提出了4种优化模型,并采用COMSOL软件对4种开关模型进行机电仿真分析,由于金的杨氏模量为70 GPa相对较小,泊松比ν为0.44,在几何参数一致的情况下具有相对较小的弹性系数,所以选择金作为悬臂梁材料。与图3(a)中的一字型悬臂梁模型对比,图4(a)为增大局部驱动面积的十字型悬臂梁模型;图4 (b)~(d)分别为未增大局部驱动面积但是降低了弹性系数的三叉戟型、蟹钳型和折叠型的悬臂梁模型(左边一列为4种优化的悬臂梁模型的俯视图,其尺寸都标注在图中,右边一列为左边模型对应的悬臂梁在不同电压下发生的形变量)。当Z方向的形变量下降了g0/3 (约为 -0.7 μm) 时对应的电压为驱动电压,从形变图中可以得到,十字型悬臂梁的驱动电压为7.2 V;三叉戟型的驱动电压为5.6 V;蟹钳型的驱动电压为3.8 V;折叠型的悬臂梁的驱动电压3.6 V。对不同的模型施加其对应的驱动电压得到的Z向位移分布如图5所示,其悬臂梁的自由端在驱动电压下向下运动,颜色标注为模型发生的形变量的大小。
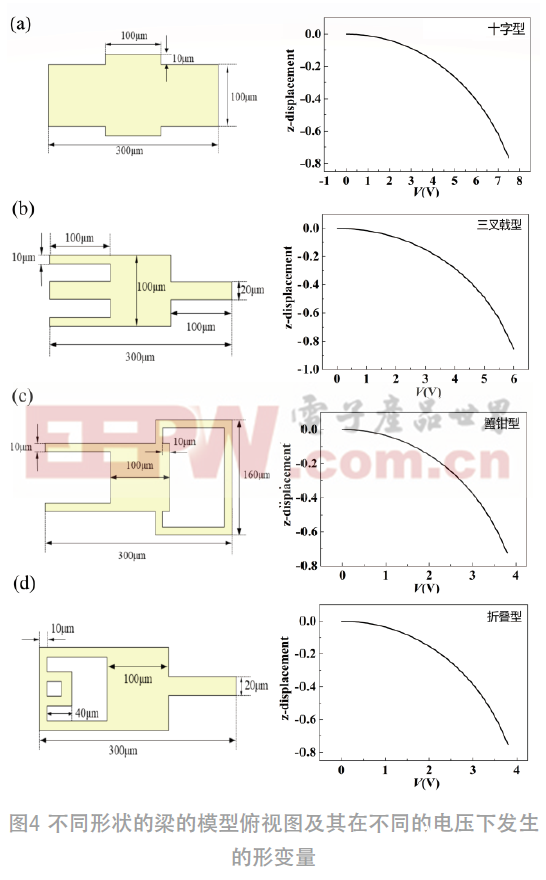
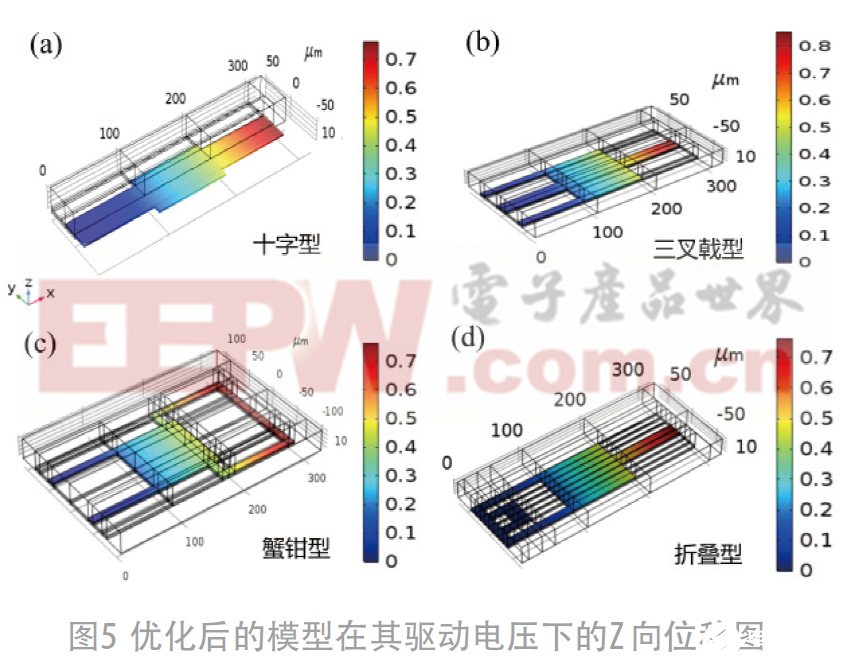
表1 中列出了不同形状的梁在不同驱动电压下的Z向位移量的具体值,并给出了不同梁的驱动电压,验证了增大局部驱动面积和降低弹性系数的悬臂梁可以减小驱动电压。然后在相同梁长的情况下对比了通过上述两种方法设计的悬臂梁的驱动电压大小,由对比结果可知,在梁长、厚度和初始间隙等参数一致的情况下,低弹性系数的梁对降低驱动电压的效率比局部增大驱动面积要高很多。
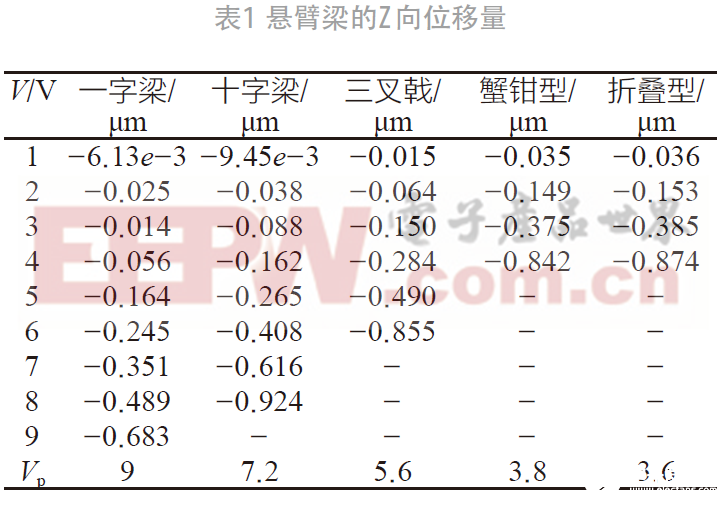
注:表中“-”意为位移量已经远大于临界不稳定状态的位移,所以没有统计。
4 结论与分析
通过理论分析和仿真,并与传统的一字型悬臂梁作对比,验证了增大局部驱动面积和降低弹性系数可以减小悬臂梁开关的驱动电压。并且降低弹性系数的悬臂梁比增大局部驱动面积的悬臂梁在降低驱动电压方面更有效。在选择低弹性系数的悬臂梁开关材料时也可以选择弹性模量较大的材料,如多晶硅、氮化硅等硅化物形成单层或者多层结构的梁,这将有利于降低成本以及工艺的可集成性。











