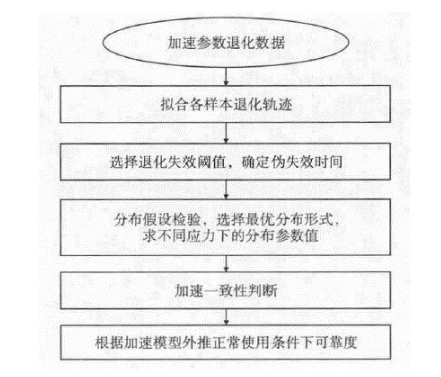
图2 加速退化轨迹评估流程
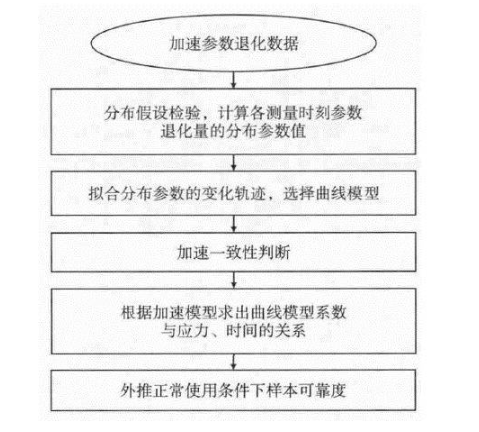
图3 加速退化量分布评估流程
基于退化轨迹拟合的方法根据各样本的加速参数退化趋势,选择适当的退化轨迹模型;根据应用需求,选择退化失效阈值,确定伪失效时间;对伪失效时间分布假设检验,选择最恰当的分布形式,估计分布参数;通过加速一致性判断,选择加速模型求出分布参数与应力的关系;外推正常使用条件下样本的总体参数及可靠度参量函数。
基于退化量分布拟合的方法是对多个样本在不同测量时刻的退化量分布规律进行建模,能够反映出参数退化量的统计特征随时间的变化规律。其主要思路是对各个测量时刻的退化数据分布假设检验,计算各个时刻参数退化量的分布参数估计值;拟合分布参数随时间的变化规律,选择曲线模型,求出各应力水平下曲线模型系数;通过加速一致性判断,选择加速模型,求出曲线模型与应力水平的关系;根据加速方程,求正常应力下满足退化失效阈值时样本的分布参数随时间的函数关系,从而得到可靠度函数。
3 MEMS陀螺仪加速参数退化可靠度评估验证实验
本文对15个MEMS陀螺仪样本开展了加速参数退化试验,图4是根据样本在三组高温应力(T=70 ℃,100 ℃,120 ℃)下加速退化试验中零偏值变化情况绘制的退化轨迹,结合应用背景,假设该样本的退化失效阈值是增加3%(即D f = 3),正常工作温度为T 0 =25 ℃。应用上述加速参数退化的可靠度评估方法对其进行可靠度评估。
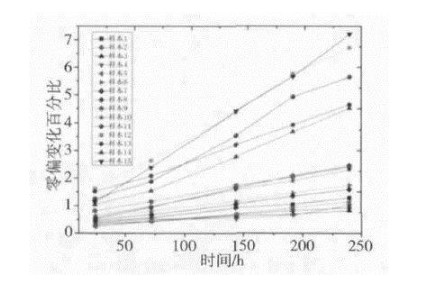
图4 不同应力下样本的参数退化轨迹
3.1 基于退化轨迹的拟合方法
根据图4估计所有应力水平下所有样本的退化轨迹模型参数,外推每个样本到达退化失效阈值的时间,并分布假设检验,结果如图5所示。三个应力下假设检验AD统计量值分别为2.48,2.683,2.4(Weibull分布),2.357,2.511,2.332(正态分布)。Weibull分布适应性较好,正态分布计算相对简单。因此应用两种分布形式的统计分析方法对所得到的退化伪失效时间分析。











