根据数字信号处理的理论,设2个光谱经光电转换采样后分别为X(i)和Y(i)(i=1,2,3,…,N,表示波长),二者互相关运算定义为

式中j为加在x上的波长漂移。波长下标超出范围[1,N]的频谱视为零。根据互相关的性质,R(j)在x(i-j)和Y(i)重叠得最多,最相似的时候得到最大值。因为每个FBG反射回来的光谱都类似于高斯分布,所以,只要先采集一个基准谱,然后,与实测谱进行互相关运算,求得互相关值最大时所对应的j值,就可以得到实测谱的漂移,也就得到了Bragg波长的漂移。
可见采用相关谱法是可行的,且重要的是此方法与传统的峰值检测法相比,具有高精度的特点。峰值检测法是计算原始反射谱中的最大值,而频谱相关法则是通过相关计算,改为计算一系列对应不同漂移值的相关值中的最大值。计算每个相关值时都对许多光谱值做了相加运算,这会按相加数N的平方根的规律有效抑制实际原始光谱中的噪声,从而提高波长测量精度。由以下推导可以看出:
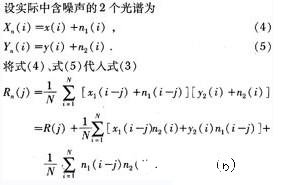
在分析前,假设n1和n2是相互独立的噪声,它们都服从高斯分布。定义信噪比SNR为信号的均方根除以噪声的均方根,设原信号Xn(i),Yn(j),的信噪比均为SNR0,根据高斯分布的独立性,式(6)的信噪比为
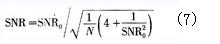
由上式可见,随着N的不断增加,相对于原信号信噪比来说,经过相关谱法后的信噪比在不断增加(理论上是这样,实际中后面实验说明),所以,原始光谱中的噪声引起的测量误差就可以被抑制。
为了降低系统硬件实现难度,保证解调速度,使波长测量精度进一步提高,本文还结合了线性插值的方法,整个的工作过程就是先在原始的光谱中每相邻两点问线性插入一些点,再利用相关谱法得到Bragg波长漂移。采用线性插值的目的就是为了使原始光谱更加相似于漂移后的光谱,从而在相关谱法中更能精确地确定波长漂移量。
3、实验结果

解调系统装置如图1,采用中心波长为1 550 nm的发光二极管(LED),谱宽为30 nm,LED发出的光经过3 dB耦合器后进入FBG,FBG反射回的光再次经过这个3 dB耦合器后进入F-P可调谐滤波器(FOOL2上型),再经光电转换、放大、D/A转换器进入数字信号处理器(DSP)实现插值-相关谱法解调(FBG0是固定波长的参考FBG,这个波长基准器可以消除可调谐F-P滤波器腔长漂移对测量精度的影响)。











