(公式2)
如果失真积和混叠信号能量保持在本底噪声以下,则SINAD= SNR。在此情况下,公式2 只是公式1 对N 求解的调整形式。更常见的情况是SINAD n(i)是来自起作用源的噪声,作用源处于由m 个不相关源组成的系统内。
起作用噪声源之一来自采样时钟边沿时序的不确定性,产生孔径抖动噪声。可以说,该噪声得出采样器正在针对移动目标捕捉交流信号的事实。采样边沿时序的变化导致采样器捕捉幅度的统计分布,即噪声(图3)。信号频率越高,信号斜率或压摆率越大,因此边沿时序既定变化导致的幅度误差越大。这样,既定孔径抖动量的效果便取决于信号频率。
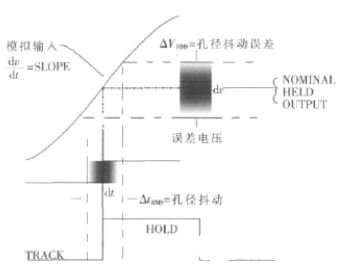
图3:孔径抖动(采样时间上的不确定性)产生噪声幅度,由于抖动时间内的信号压摆,该幅度取决于信号频率。
由孔径抖动引起的SNR 为
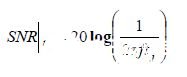
(公式3)
其中f 是信号频率,tj 是均方根孔径抖动。通常在挑选ADC时,问题在于目标应用在既定频率信号的SNR 要求下可以容忍的最大幅度抖动。整理公式3 得出
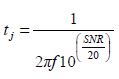
(公式4)
请注意,除了转换器内的抖动源外,您的应用电路内也有抖动源。因此,电路实现的净性能与转换器选择和设计其他方面(通常是时钟产生电路和电路板布局)的品质都有关系。
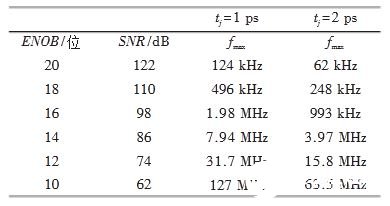
为了解抖动影响既定ENOB 最大信号频率的程度,可分别来看1 ps 和2 ps 抖动噪声远超其他性能限制参数的两个系统。整理公式4,我们可以针对既定抖动计算产生指定ENOB(或SNR)的最大信号频率。
表1. 对比抖动时间相差两倍的系统
失真积
信号链内的非线性造成了许多失真积,通常是HD2(第二谐波失真)、HD3(第三谐波失真)、IMD2(二阶交调失真)和IMD3(三阶交调失真)。线性电路内的失真倾向于随信号接近有源元件线性工作范围的极限而逐渐增加。在代码空间突然结束的ADC 内则不是这样。
因此,重要的是输入跨度内有足够的范围容纳您要进行低失真量化的预期输入幅度,特别是在处理复杂宽带信号时。最终,选择标称输入幅度是为了平衡信号跨度余量,避免限制优化SNR 的需要。











