低通滤波器
低通滤波器的基本电路特点是,只允许低于截止频率的信号通过。
(1)一阶低通Butterworth滤波电路
下图a和b是用运算放大器设计的两种一阶Butterworth滤波电路的电路。图a是反相输入一阶低通滤波器,实际上就是一个积分电路,其分析方法与一阶积分电路相同。
基本滤波电路 演示
图b是同相输入的一阶低通滤波器。根据给定的电路图可以得到

对滤波器来说,更关心的是正弦稳态是的行为特性,利用拉氏变换与富氏变换的关系,有

下图是上式RC=2时的幅频特性和相频特性波特图。
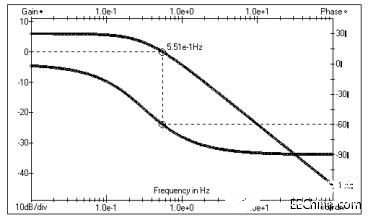
RC=2时一阶Butterworth低通滤波器的频率响应特性
(2)二阶低通Butterworth滤波电路
下 图是用运算放大器设计的二阶低通Butterworth滤波电路。

二阶Butterworth低通滤波电路
直接采用频域分析方法得到
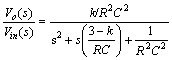
其中k = 1+R1/R2 。令Q=1/(3-k),w0=1/RC,则可以写成
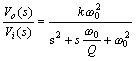
其中k相当于同相放大器的电压放大倍数,叫做滤波器的通带增益,Q叫做品质因数,w0叫做特征角频率。
下图是二阶低通滤波器在RC=2时的波特图,其中图a是Q》0.707时的效果,图b是Q=0.707时的效果,图c是Q《0.707时的效果。

(a) Q》0.707

(b) Q=0.707

(c)Q《0.707
二阶低通滤波器在RC=2时的波特图
从图中可以看出,当Q》0.707 或Q《0.707时,通带边沿处会出现比较大的不平坦现象。因此,品质因数表明了滤波器通带的状态。一般要求Q=0.707。











