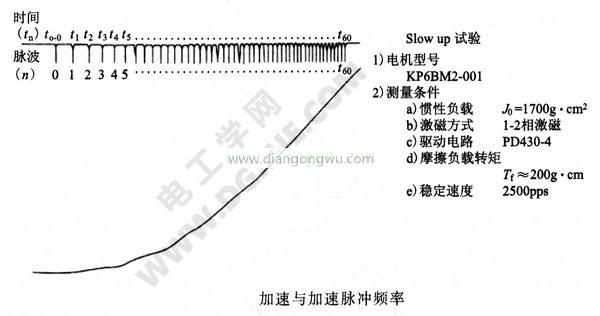
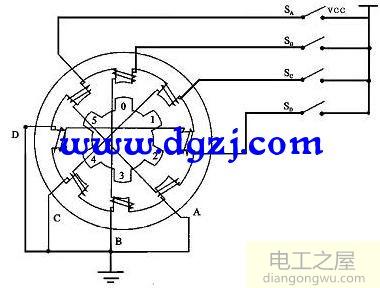
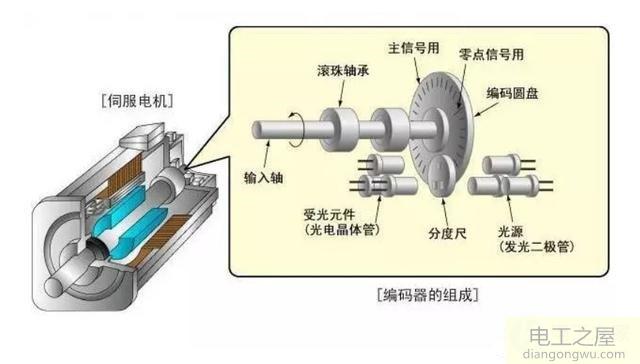
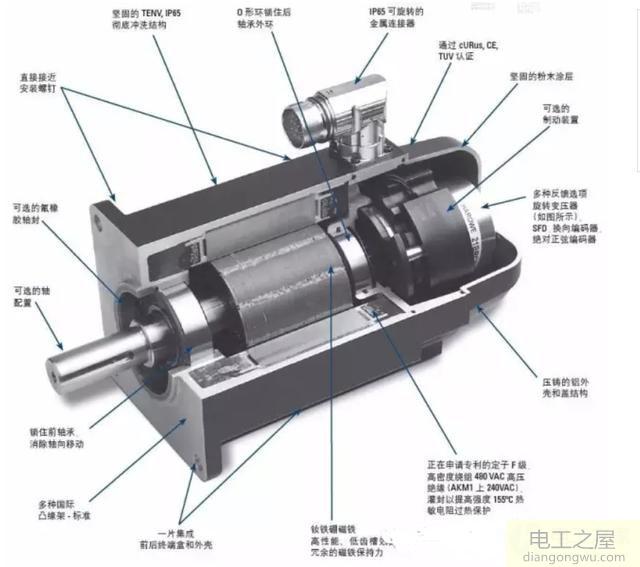
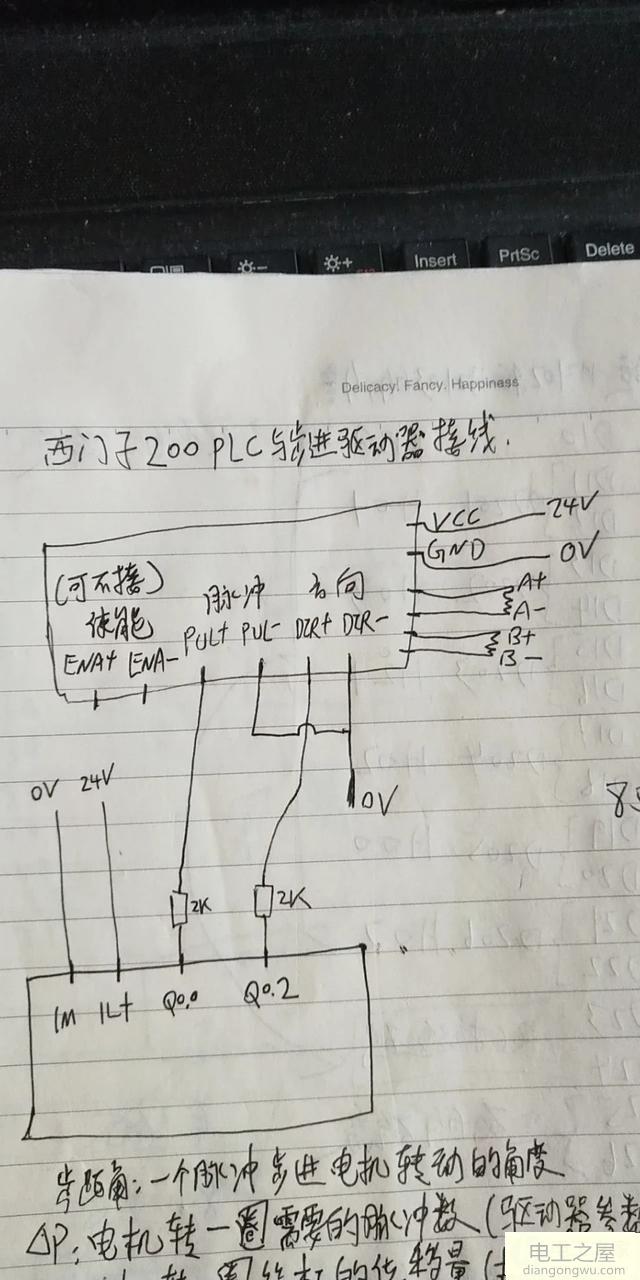
步进电机驱动负载可以按希望的速度起动,若驱动速度超过自身起动脉冲频率时,此速度下则不能起动。因此,只有比电机起动脉冲频率低的速度指令才能起动。采取加速的方法使速度线性增加到所希望的速度,此种方法称为慢速加速驱动。下图表示步进电机的加速与速度-转矩特性。
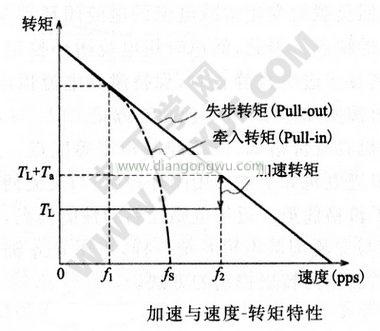
步进电机的速度-转矩特性有失步转矩(同步失步转矩)与牵入转矩(同步牵入转矩)。现在,负载转矩TL的负载要用频率f2驱动时,则自身起动脉冲频率应不大于频率f2的数值。以十分低的频率f1起动电机,然后加速达到频率f2,此时负载还包括转子惯量J,此为加速惯量,需要必要的惯量加速转矩Tα,因此这两个转矩(TL+Tα)的合成转矩成为起动到转速频率f2时所必须的转矩。此时的加速转矩为下面步进电机运动方式的第一项:
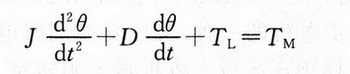
上式的D为速度比例系数,第二项因此比其他项小而忽略不计。TM为步进电机产生的电磁转矩,(TM-TL)如图上图所示,能产生加速度的转矩。速度到达f2后按设定的转速旋转一段时间,然后减速到f1,形成速度包络线,此时的减速运转称为减速驱动,此种速度曲线称为梯形驱动。该速度包络线与其速度相对应的转矩特性见下图。
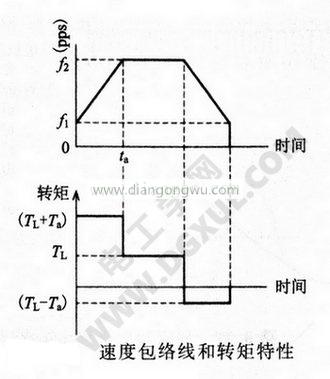
此梯形面积相当总步数,电机轴在横轴的时间内,转过相当梯形面积的步距角,把负载拉到相应的位置上。设加速时间为ta,步距角为θs,则加速转矩用下式表示:
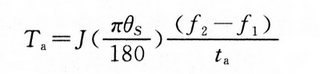
步进电机的失步转矩为该电机能产生的最大转矩,由前文《步进电机:细分步进驱动》中的下式可知, 负载角δ=π/2时为产生失步转矩的时刻,电机到达f2速度时,电机转矩只加TL负载,在速度f2与TL平衡的功率角为δ,电机产生的转矩Ta分量减少。
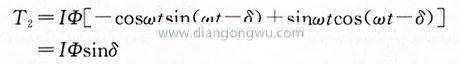
减速时如图示,也产生反方向转矩。此时,负载角δ变成负,产生反方向转矩。加速时的加速脉冲频率如下图所示,各梯形面积S由加速时间来决定,即各个梯形面积S等于步距角。
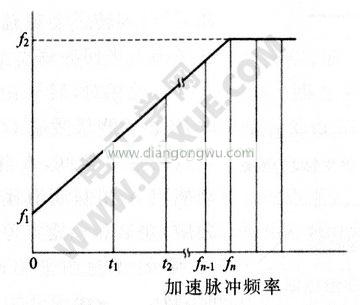
下图所示为两相HB型1.8°步进电机由静止时开始加速(Slowup)的加速曲线。此为步进电机的梯形驱动曲线,电机能快速达到目标位置,而不会出现失步现象。