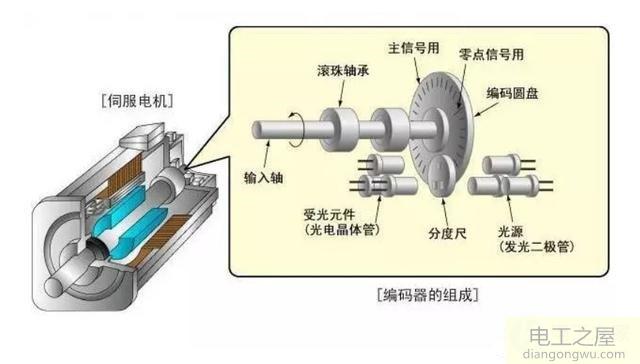
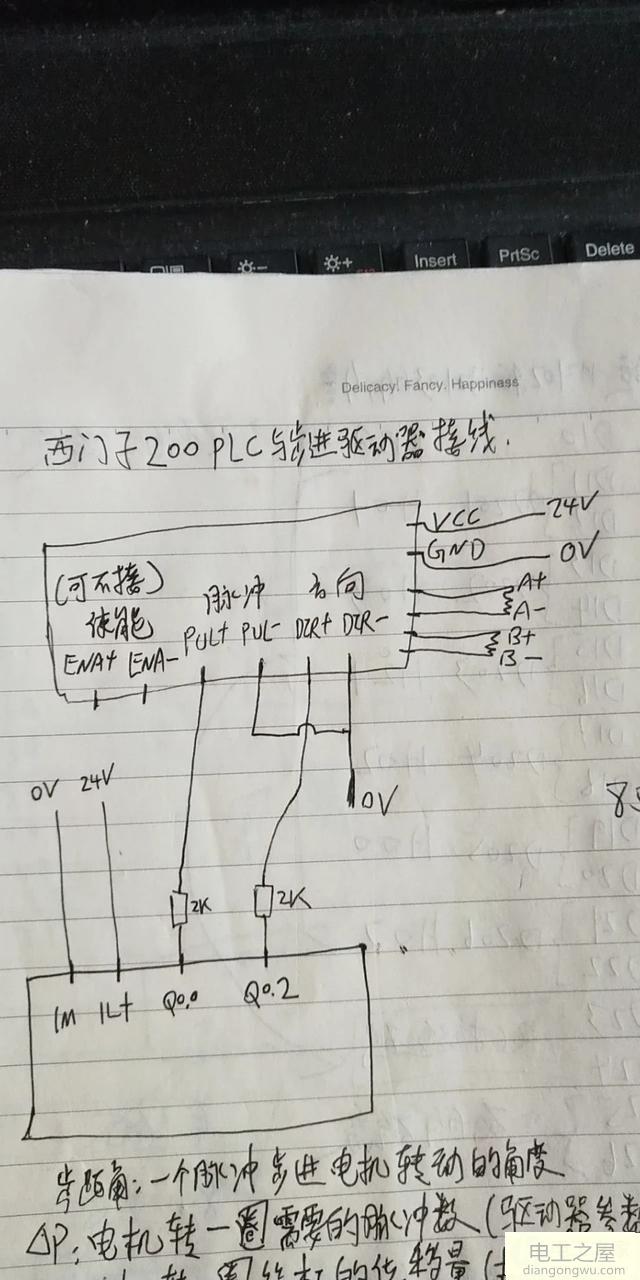
关于交流电机的矢量控制技术,有很多论文与各种文章介绍。但多用难解的公式与坐标来记述,如果没有扎实的数学和控制等理论基础的话,相信大家有同感比较难理解。日笃君尽量用简单易懂的图解与计算来聊聊电机的构造,静止坐标与旋转坐标的变化,矢量控制,伺服控制等电机驱动技术。
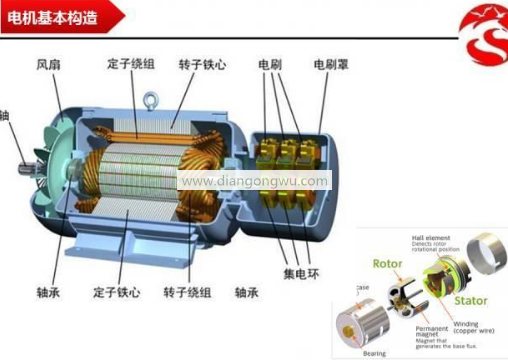
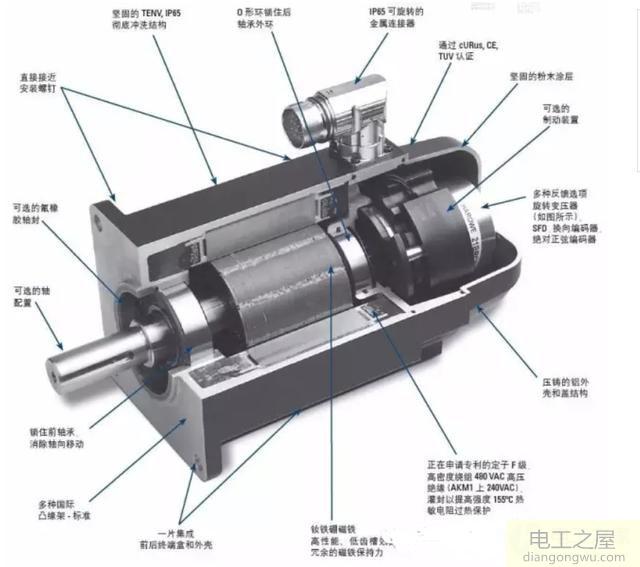
在聊控制之前,为了更好理解控制,我们先来看看电机的构造。实时应用的电机构造很复杂,但可以简单的理解成:电机由装在里面的转子与装在外面的定子构成(也有相反的电机),转子里面一般放入永久磁石,定子里面一般缠绕铜线。然后在中间插入中轴来带动驱动物体。
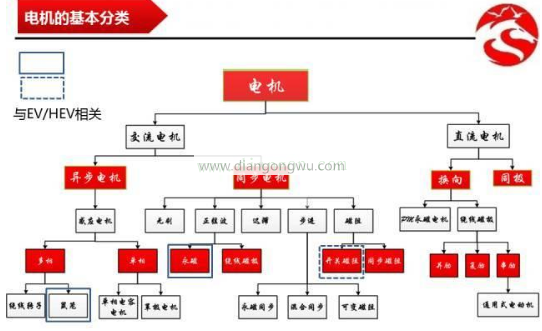
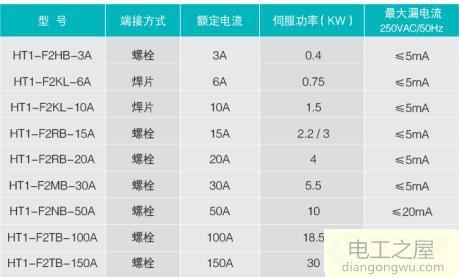
电机技术经过百年的发展,形成了如上的各种分类。电机上使用的磁石属于稀有金属,产量主要分布在中国,近年由于稀土材料的价格高腾,工业界正在积极研究如何减少稀土的使用量,保持性能的同时降低产品成本,是企业也更是工程师永远的课题。如今实际应用中,同步电机得到广泛的采用。
同步电机又以磁石所装入的部位,主要分类为SPM(表面磁石)和IPM(内部磁石):
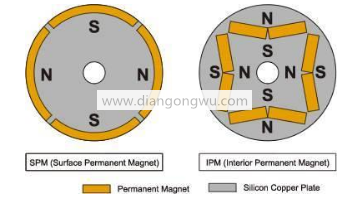
SPM电机由于控制简单,早起被工业界所采用,但是这种电机由于磁石装在转子的表面,所以可以利用的动力主要来源于自身的表面磁石。
IPM电机由于可以利用磁石与磁石周围励磁的动力,产生高密度的能量,而且可以通过构造的工夫减少稀土的使用量,所以今年得到更广泛的应用。
SPM电机:

转子(磁石未插入状态)

定子(线圈缠绕状态)
我们可以看到,定子铁芯上有斜入的空心,在这里缠绕线圈。斜着是应为可以使磁场平均化(具体请参照相关论文或专利)。

转子与定子的合体
IPM电机:

转子(磁石未插入状态)
我们可以看到装磁石的地方分为对称的两条,这是应为想使得励磁的地方得到有效的利用,这个空心对称的角度会影响励磁动力,具体有兴趣的话可以参照各种专利(关于角度问题有很多专利申请)。

定子(线圈缠绕状态)


转子与定子的合体
下面进入正题,聊聊交流电机的控制问题。
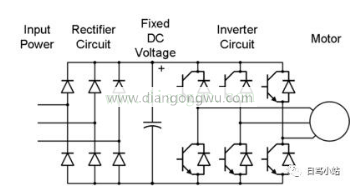
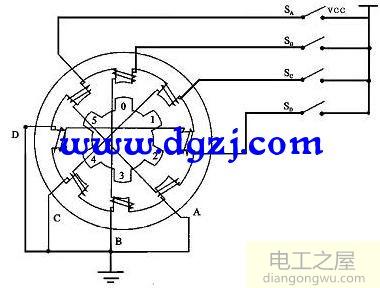
一般的电机驱动变频器如上所示。我们可以看到IGBT的输出与电机的输入都是三相(电压,电流的UVW),而电机里面的磁石只有S和N的两极。同时,三相的UVW属于静止坐标,而电机在运行时属于旋转坐标,那么我们要控制电机就需要按照我们的目的把三相的静止坐标与二相的旋转坐标进行互换。
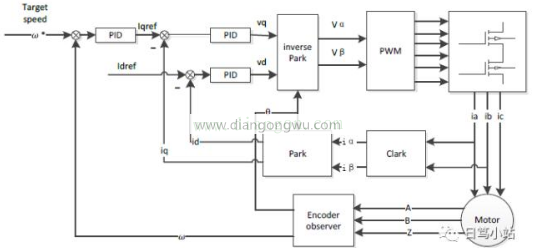
我们先来俯瞰一下矢量控制的结构图:
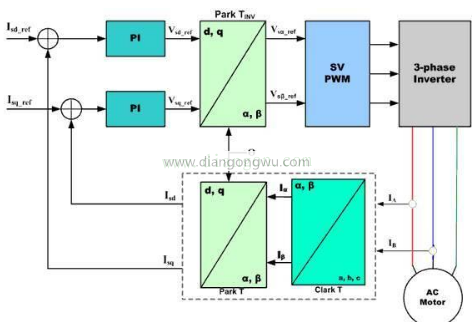
从AC Motor的电流采样得到三相交流数值,通过Clark变换成二相坐标(αβ),再利用Park变换把静止的αβ坐标换成旋转的dq坐标,形成反馈值,与dq的指令值进行演算。
通过PI控制器的演算结果,我们可以得到dq两相的电压指令值,把旋转坐标的dq指令值通过逆Park变换,得到静止坐标的αβ,再通过逆Clark变换得到三相的电压驱动指令,控制SVPWM的输出。
另外,d轴对应励磁所产生的转矩,q轴对应永久磁石所产生的转矩。在SPM电机的控制时我们可以让d轴的指令值为0。但在IPM电机控制时,d轴和q轴都要利用,所以在速度环需要有两个指令的输出。
下面以正向Clark变换和Park变换,来计算如何进行坐标变换的:
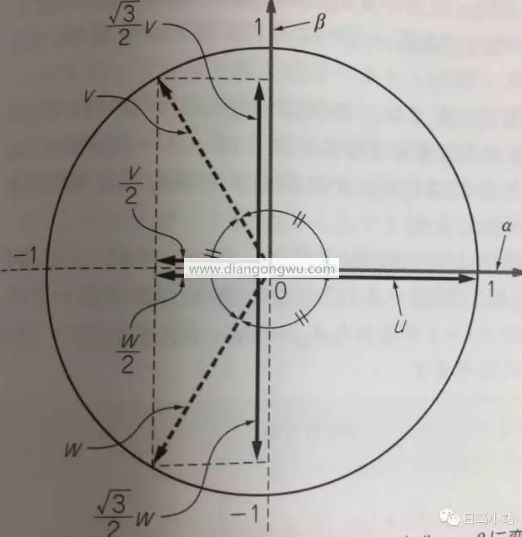
Clark变换
我们设定U和α轴一致,并假设k为三相与二相的矢量振幅比系数。通过上面图示我们可以得到:
α = k{ U - 1/2V - 1/2W}
β = k{ sqrt(3)/2V - sqrt(3)/2W }
由于三相平衡,我们可以有:
U + V + W = 0
α = U
带入上式可以得到: k = 2/3
所以β = 1/sqrt(3)*(V-W) = 1/sqrt(3)*(U+2V)
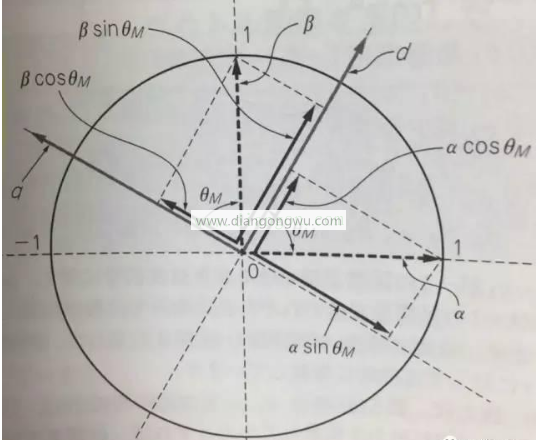
Park变换
我们假设αβ轴与dq轴之间有着θ的角度,把αβ分解到dq轴上,再利用三角公式可以得到:
d = αcosθ + βsinθ
q = -αsinθ + βcosθ
旋转坐标与静止坐标的逆变换同上述一样,这里就省略了。
上面我们聊了坐标变换与矢量控制结构,矢量控制的目的是控制伺服的同时,使电流与电压的位相一致进而提高电力效率和电机转矩的效率。下面我们再来了解下包括矢量控制在内的伺服控制结构。
上述结构可以简化为以下:位置控制环,速度控制环,矢量(电流)控制环。
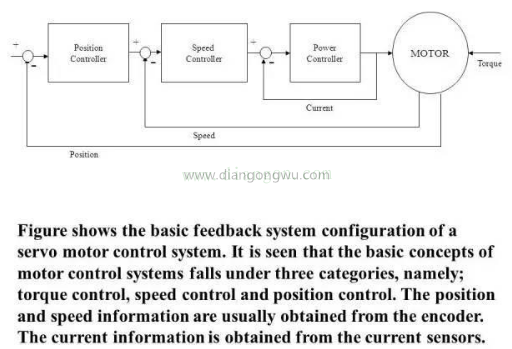
浅析了交流电机的矢量控制,实际利用变频器的交流电机控制中,由于外乱,温度,高频等等因素的影响,使得电机控制算法越来越复杂,精度越来越高,但我们只要掌握了上述最基本的方法,有助于理解其他发展算法。