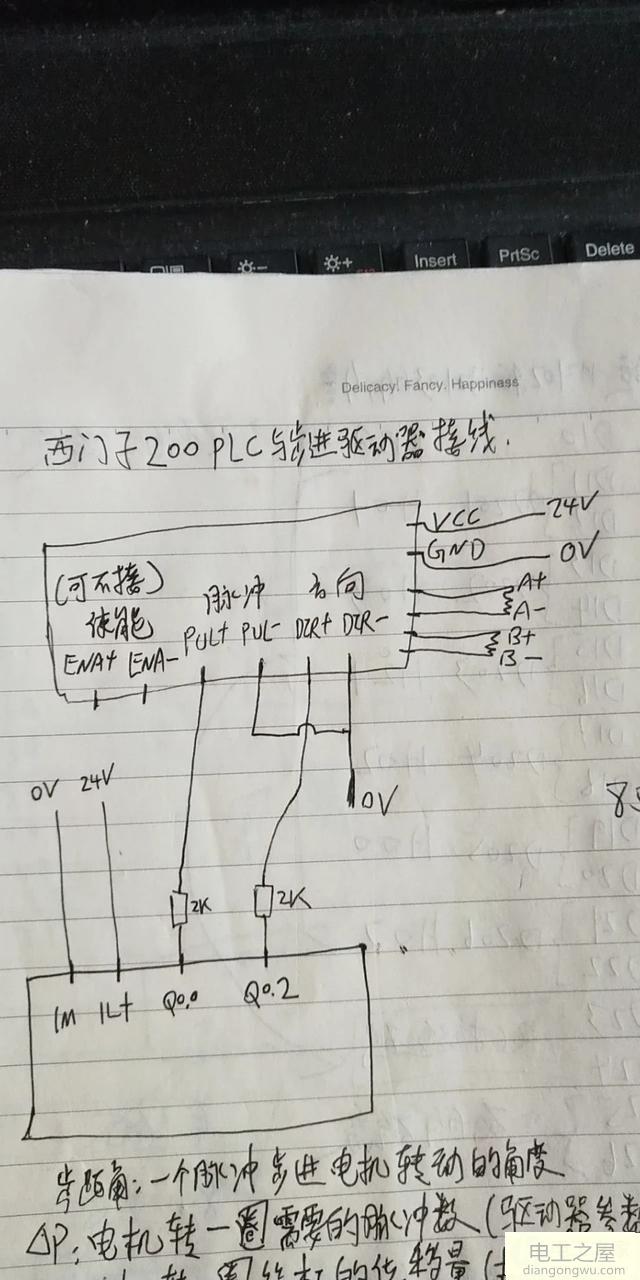
算法对于步进电机调速系统设计是一个相当重在的环节,因为只有确定了算法之后才能对步进电机的速度进行准确的控制,并时也能达到精确的调速目的。同时算法也是编写软件的前提与基础。控制算法有多种,常用的两种算法是PID和模糊控制算法。
PID 控制与模糊控制是两种常用的控制方法,但它们还存在一些不足,如一般PID 控制容易产生超调、模糊控制的稳态精度不高,在这两种控制方法基础上进行改进,可产生多种更好的控制方法。本文采用的复合PID 控制算法和带动态补偿的模糊控制算法克服了以上缺陷,取得了较好的实验效果。
1、PID 控制算法
PID 调节的实质就是根据输入的偏差值,按比例、积分、微分的函数关系,进行运算,将其运算结果用以输出控制,将基本PID 算式离散化可得到位置型PID 控制算法,对位置型PID 进行变换可得到增量型PID 控制算法。对控制精度要求较高的系统一般采用位置型算法,而在以步进电机或多圈电位器做执行器件的系统中,则采用增量型算法。
PID是一种工业控制过程中应用较为广泛的一种控制算法,它具有原理简单,易于实现,稳定性好,适用范围广,控制参数易于整定等优点。PID控制不需了解被控对象的数学模型,只要根据经验调整控制器参数 ,便可获得满意的结果。其不足之处是对被控参数的变化比较敏感。但是通过软件编程方法实现PID控制 ,可以灵活地调整参数。,尽管近年来出现了很多先进的控制算法,但PID控制仍然以其独有的特点在工业控制过程中具有相当大的比重,且控制效果相当令人满意。
连续PID控制器也称比例-积分-微分控制器,即过程控制是按误差的比例(P-ProportionAl)、积分(I-IntegrAl)和微分(D-DerivAtive)对系统进行控制,其系统原理框图如图1所示:
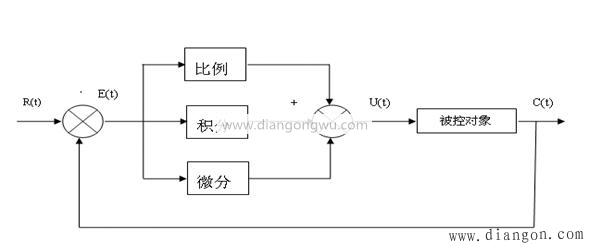
图1 PID的原理框图
它的控制规律的数学模型如下:
![]() \* MERGEFORMAT
\* MERGEFORMAT 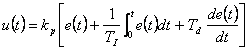 \* MERGEFORMAT (1)
\* MERGEFORMAT (1)
或写成传递函数形式:
 \* MERGEFORMAT (2)
\* MERGEFORMAT (2)
式中,e(t):调节器输入函数,即给定量与输出量的偏u(t):调节器输出函数。
Kp:比例系数;
T:积分时间常数;
T:微分时间常数。
将式(2-1)展开,调节器输出函数可分成比例部分、积分部分和微分部分,它们分别是:
⑴ 比例部分比例部分的数学表达式是![]() \* MERGEFORMAT ,p在比例部分中,Kp是比例系数,Kp越大,可以使系统的过渡过程越快,迅速消除静误差;但Kp过大,易使系统超调,产生振荡,导致不稳定。因此,此比例系数应选择合适,才能达到使系统的过渡过程时间短而稳定的效果。
\* MERGEFORMAT ,p在比例部分中,Kp是比例系数,Kp越大,可以使系统的过渡过程越快,迅速消除静误差;但Kp过大,易使系统超调,产生振荡,导致不稳定。因此,此比例系数应选择合适,才能达到使系统的过渡过程时间短而稳定的效果。
图为比例调节器

![]() (3)
(3)
比例调节器
其中: U控制器的输出
![]() \* MERGEFORMAT 比例系数
\* MERGEFORMAT 比例系数
E 调节器输入偏差
![]() \* MERGEFORMAT 控制量的基准
\* MERGEFORMAT 控制量的基准
比例作用:迅速反应误差,但不能消除稳态误差,过大容易引起不稳定
⑵ 积分部分 积分部分的数学表达式是![]() \* MERGEFORMAT 从它的数学表达式可以看出,要是系统误差存在,控制作用就会不断增
\* MERGEFORMAT 从它的数学表达式可以看出,要是系统误差存在,控制作用就会不断增
加或减少,只有e(t)=0时,它的积分才是一个不变的常数,控制作用也就不会改变,积分部分的作用是消除系统误差。
积分时间常数![]() \* MERGEFORMAT 的选择对积分部分的作用影响很大。
\* MERGEFORMAT 的选择对积分部分的作用影响很大。![]() \* MERGEFORMAT 较大,积分作用较弱,这时,系统消除误差所需的时间会加长,调节过程慢;
\* MERGEFORMAT 较大,积分作用较弱,这时,系统消除误差所需的时间会加长,调节过程慢;![]() \* MERGEFORMAT 较小,积分作用增强,这时可能使系统过渡过程产生振荡,但可以较快地消除误差。
\* MERGEFORMAT 较小,积分作用增强,这时可能使系统过渡过程产生振荡,但可以较快地消除误差。
⑶ 微分部分
微分部分的数学表达式是![]() \* MERGEFORMAT .
\* MERGEFORMAT .
微分部分的作用主要是抵消误差的变化,作用强弱由微分时间常数T确定。![]() \* MERGEFORMAT 越大,则抑制误差e(t)变化的作用越强,但易于使系统产生振荡;
\* MERGEFORMAT 越大,则抑制误差e(t)变化的作用越强,但易于使系统产生振荡; ![]() \* MERGEFORMAT 越小,抵消误差的作用越弱。因而,微分时间常数要选择合适,使系统尽快稳定。
\* MERGEFORMAT 越小,抵消误差的作用越弱。因而,微分时间常数要选择合适,使系统尽快稳定。
比例积分微分调节器如图2所示:
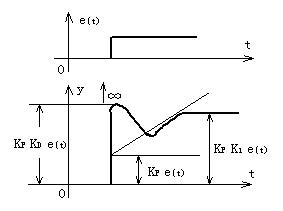
图2
但PID算法有两种分别为: 位置式、增量式.
位置式PID控制算法
![]()
![]()
![]()
(4)
(5) 由(5)与(6)式可以推出下式
![]() (6)
(6)
位置式控制算法提供执行机构的位置uk,需要累计Ek.
增量式PID控制算法
![]() (8)
(8)
![]() (9)
(9)
由(1)与(2)式可推出下式:
![]() (10)
(10)
增量式控制算法提供执行机构的增量![]() \* MERGEFORMAT 只需要保持.现时以前3个时刻的偏差值即可.增量式算法不需做累加,计算误差和计算精度问题对控制量的计算影响较小;位置式算法要用到过去偏差的累加值,容易产生较大的累计误差。
\* MERGEFORMAT 只需要保持.现时以前3个时刻的偏差值即可.增量式算法不需做累加,计算误差和计算精度问题对控制量的计算影响较小;位置式算法要用到过去偏差的累加值,容易产生较大的累计误差。
控制从手动切换到自动时,位置式算法必须先将计算机的输出值置为原始值![]() \* MERGEFORMAT 时,才能保证无冲击切换;增量式算法与原始值无关,易于实现手动到自动的无冲击切换。
\* MERGEFORMAT 时,才能保证无冲击切换;增量式算法与原始值无关,易于实现手动到自动的无冲击切换。
在实际应用中,应根据被控对象的实际情况加以选择。一般认为,在以闸管或伺服电机作为执行器件,或对控制精度要求较高的系统中,应当采用位置式算法;而在以步进电机或多圈电位器作执行器件的系统中,则应采用增量式算法。
因本次设计对步进电机的调速范围与控制精确的要求,应采用增量式PID控制:系统的流程框图如2所示:
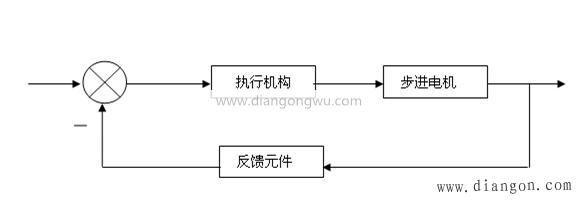
图2 步进电机调速系统的控制流程图