在实际应用中,二阶线性系统常采用阻尼因子ξ、无阻尼振荡频率ωn描述。在二阶二型锁相环中,τ1,τ2 ,K 与ξ,ωn之间的对应关系如下:
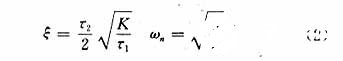
在式(1)和式(2)的基础上对图2进行等效变换,可以得到软件锁相环的另一个线性相位Z域模型,如图3所示。
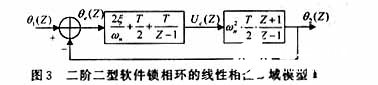
在模型Ⅰ中,参数τ1,τ2和K与实现电路功能的电阻、电容、压控振荡器密切相关。而实现软件锁相功能的却是乘法器、加法器与寄存器,因此采用模型Ⅱ表征软件锁相环线性相位Z域模型显得更有实际意义。
2 软件锁相环的数学模型
数字鉴相器的Z域模型如下:
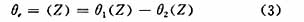
实现数字鉴相器的方法之一就是借助信号的正交分解,图4是该方法的原理框图。
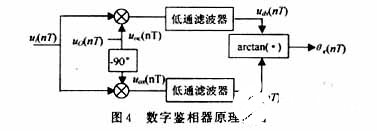


如果以数字频率描述数控振荡器,则称其数字中心频率为ω0T,数字偏置频率为ωn2·uc(nT)·T。因此,该数控振荡器的灵敏度与数字灵敏度分别为·T。
3 多速率条件下的软件锁相环
在数字化接收机中,经常碰到多速率条件下的抽样率转换问题。所谓多速率系统是指在一个数字系统中存在2个或2个以上的抽样率。构成软件锁相环鉴相器的混频器通常工作在系统采样频率上。在满足奈奎斯特采样定律的前提下,数字化接收机的系统采样率一般高达数10 M。而数字鉴相器组成部分的反正切表,由于混频之后的数据经过多倍抽取,工作频率已经下降到与信号波特率相近的水平。数据抽取同时也降低DSP的运算量,由DSP完成的环路滤波的处理速度近似等于信号波特率。此外由于软件锁相环中的数控振荡器需要给混频器提供同样速率的正交载波,其工作速率与混频器相等,需要进行内插来调整速率。
为了合理利用DSP有限的计算资源,总是在满足同步需要的前提下尽可能地降低环路滤波的工作速率,也就是通常所说的环路频率。环路频率是软件锁相环的一个重要参数,他同时决定着锁相环算法的计算量与捕获速度。环路频率过高将带来额外的计算负担,环路频率太低又不能满足捕获速度的需要,在应用中通常取系统波特率作为环路频率的大小。该扩展模型对应的线性相位Z域模型如图5所示。











