通过按比严格需要的频率更高的频率采样,能够收集更多的样本。然后采用平均滤波器对所有ADC数据进行后处理,原因有二:
·每4个平均样本,噪声降低1位。
·平均滤波器转换函数是一个低通滤波器。当∑-∆架构将其量化噪声推向高频时,应该移除平均滤波器转换函数,如图3所示。所以,本次滤波由这个平均滤波器完成。
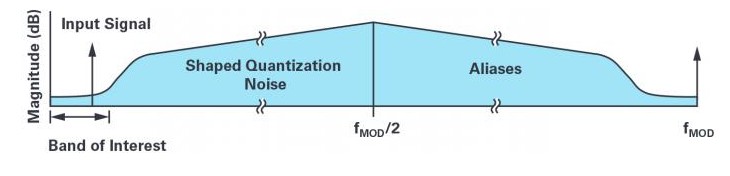
图3.∑-∆噪声整形。
样本的平均数量,即抽取率(N),会决定输出数据速率(ODR),输出数据速率是ADC提供转换结果的速率,单位为样本/秒,如公式1所示。抽取率通常是整数,带有一组可在数字滤波器上离散编程的预定义值(即N=32、64、128等)。因此,通过保持fMOD常量,ODR将根据预定义值集内的N值进行配置。

平均过程通常由一个sinc滤波器在内部实现,调制器的模拟转换开始脉冲也在内部生成,因此不会从外部管控转换过程触发。这种类型的转换器实际会连续采样,跟踪输入信号,并处理获得的数据。一旦该过程(采样和平均)完成,转换器就会生成一个数据就绪信号,告知控制器数据可以通过数字接口回读。
如图4所示,∑-∆的工作流程可以概括为四个主要步骤:
·调制器以fMOD频率对信号采样。
·通过sinc数字滤波器对样本进行平均。
·对sinc滤波器提供的数据进行偏移和增益校正。
·数据就绪引脚切换,表示转换结果已就绪,可由控制器回读。
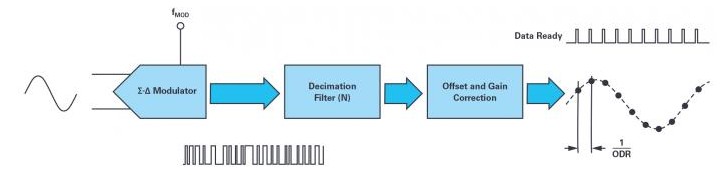
图4.Σ-ΔADC工作流程图。
由于没有从外部控制何时触发内部采样,所以如果要对分布式系统中的多个Σ-ΔADC进行同步,必须同时对所有数字滤波器实施复位,这是因为平均转换启动是由数字滤波器控制的。
图5显示在所有Σ-ΔADC都采用相同的ODR和fMOD的情况下,对同步产生的影响。
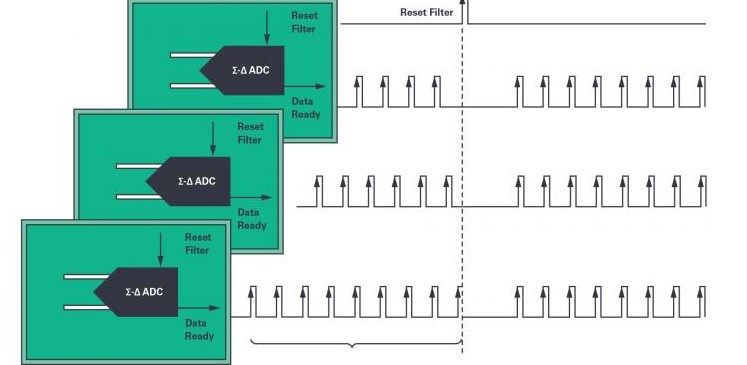
图5.∑-∆系统复位同步。











