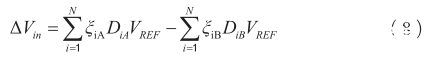这种基于参考ADC的LMS校正算法增加了电路的面积、功耗、以及复杂度,一种改进的方案是采用分裂式ADC的LMS算法。即把原来的ADC分为两个结构相同的ADC,电容值减半,两个子ADC同时对输入信号进行采样和量化,输出的平均值作为系统最终的输出。虽然电容值减半噪声会随之加倍,但平均操作也会使噪声减半,因此噪声和功耗相比原ADC不会增加。
当一个N位的ADC在量化结束后,输入信号模拟值可表示为:

式中, D i 代表每一位量化后的码字, ω i 为该位对应的权重值,V REF 为电容阵列的参考电压。当电容没有失配时, ω i 组成一组二进制权重序列,如果不考虑其他非理想因素, D i 就是输入信号 V in 正确的量化后的码字。但由于电容在制造过程中存在随机失配,权重 ω i不再是二进制权重序列,非理想的权重序列会导致量化码字出错,从而无法还原出真实的模拟输入信号。
采用分裂式ADC的框架图示意图如图2.1所示。
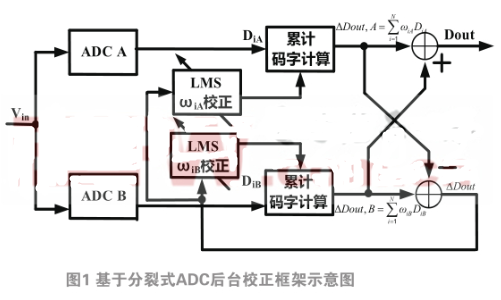
图中分裂式SAR ADC包括两个ADC子模块,每个ADC模块中DAC电容阵列采用非二进制编码电容阵列,两个ADC分别对同一输入信号进行采样和量化,它们的失配情况互不相同。
假设分别的实际权重为 ω iA 和 ω iB ,则输入信号可分别表示为:
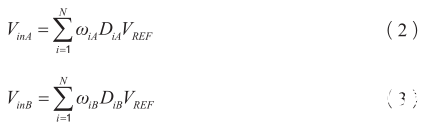
如果将实际权重表示为理想权重 ω i,ideal和误差权重ξ i 的和,则:

因此可以根据两个ADC量化后输出的码字将输入信号重写为:
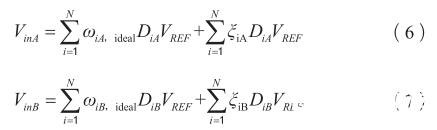
因为两个ADC是对同一个模拟输入信号进行采样和量化,在不断迭代权重更新后,量化码字D iA 和D iB 会趋于相等,所以量化后的输入模拟差值可表示为;